O perimeter of the square and the measurement of the contour of this geometric figure. Remember that a square is a polygon with four sides of the same length. This means that its perimeter will be the sum of four congruent sides.
consider The the length of the side of a square. So the perimeter of this square will be \(a+a+a+a = 4a\).
Read too: What are quadrilaterals?
Summary about perimeter of square
A square is a polygon with four congruent sides and four right angles.
The perimeter of a square is the sum of the four sides.
If the side of the square measures The, the perimeter is given by
\(P_{square} =a+a+a+a=4a\)
The diagonal of a square on one side The is given by
\(d_{square} =a\sqrt2\)
The area of a square on one side The is given by
\(A_{square} =a⋅a=a^2\)
How to calculate the perimeter of the square?
To calculate the perimeter of the square, just know the measurement of your side The and substitute in the sum of the sides of the figure.
Example:
What is the perimeter of a square with a side of 3 cm?
\(P_{square} =3+3+3+3 = 4 ⋅3 = 12\ cm\)
Perimeter of square with unknown sides
But what if the side of the square is unknown, that is, if the value of The not expressed? In that case, you need to use other information about the square to first determine the length of the side and then calculate the perimeter.
Let's see an example of how to calculate the perimeter of the square from the diagonal measurement. Remember that the diagonal of the square is the segment with endpoints at non-consecutive vertices.
Example:
Find the perimeter of a square whose diagonal is 52 cm.
The diagonal of a square on one side The is obtained by the expression
\(d_{square} =a\sqrt2\)
Therefore,
\(5\sqrt2 \ cm=a\sqrt2\)
\(a = 5\ cm\)
So the perimeter of this square is
\(P_{square} = 4⋅5 = 20\ cm\)
See too: Polygons inscribed in circles
How to find the perimeter of a square inscribed in a circle?
If a square is inscribed in a circle, then the four vertices of the square belong to the circle. Look at the image below, where a square of side The is inscribed in a circle of radius R.
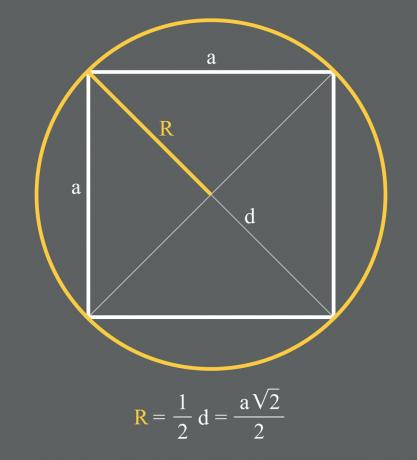
note that the radius R of the circle is half the diagonal of the square. I.e,
\(R=\frac{d}2\)
As \(d_{square} =a\sqrt2\), We have to
\(R=\frac{a\sqrt2}2\)
Thus, given a square inscribed in a circle of radius R, we can use this expression to determine the side The. From this we can calculate the perimeter of the square.
Example:
What is the perimeter of a square inscribed in a circle of radius \(R=4\sqrt2\ cm\)?
\(R=\frac{a\sqrt2}2\)
\(4\sqrt2=\frac{a\sqrt2}2\)
\(8\sqrt2=a\sqrt2\)
\(a=8\ cm\)
Therefore,
\(P_{square} = 4⋅8 = 32\ cm\)
How to calculate the area of the square?
The area of a square is the region that this polygon occupies in the plane. To calculate this measure, enoughmultiply the lengths of adjacent sides:
\(A_{square} =a⋅a=a^2\)
Example:
What is the area of a square with a side of 7 cm?
\(A_{square} =a^2\)
\(A_{square} =7^2=49\ cm^2\)
Know more: Formulas for calculating the area of plane figures
Solved exercises on square perimeter
question 1
If the area of a square is 81 cm², the perimeter is equal to
a) 9 cm
b) 18 cm
c) 27 cm
d) 36 cm
e) 45 cm
Resolution
\(A_{square} =a^2\)
\(81=a^2\)
\(a=\sqrt{81}=9\ cm\)
Therefore,
\(P_{square} = 4⋅9 = 36\ cm\)
Alternative D.
question 2
Consider a square inscribed in a circle whose diameter measures \(10\sqrt2\). The perimeter of the square, in cm, is equal to
a) 10
b) 12
c) 22
d) 30
e) 40
Resolution
The diameter of a circle is twice the radius. Thus, the diameter corresponds to the measure of the diagonal of the inscribed square:
\(d_{square} =10\sqrt2\)
\(a\sqrt2=10\sqrt2\)
\(a=10\ cm\)
Soon,
\(P_{square} = 4⋅10 = 40\ cm\)
E alternative.
Sources
LIMA, E. L. Analytic geometry and Linear algebra. Rio de Janeiro: IMPA, 2014.
REZENDE, E.Q.F.; QUEIROZ, M. L. B. in. Plane Euclidean Geometry: and geometric constructions. 2nd ed. Campinas: Unicamp, 2008.
By Maria Luiza Alves Rizzo
Math teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/perimetro-do-quadrado.htm
