O Schrödinger's atomic model is a common form used to designate the description of the atom by solving the Schrödinger equation, proposed by the Austrian physicist Erwin Schrödinger in 1927. The equation is conceived based on important observations obtained within quantum mechanics, bringing a robust justification for the energy of the atom and the electron.
The atom conceived by Schrödinger is based on the wave-particle duality, on the uncertainty principle, among other notions coined at the beginning of the 20th century. It brought great advances to the understanding of matter, as it paved the way for a more solid understanding of polyelectronic atoms, something that is not possible with the atomic model proposed by Bohr.
Read too: Atomic models — the models proposed to explain the structure of the atom
Topics of this article
- 1 - Summary of Schrödinger's atomic model
- 2 - What is Schrödinger's atomic model?
-
3 - Experimental basis for Schrödinger's atomic model
- Photoelectric effect
- wave-particle duality
- uncertainty principle
- 4 - Characteristics of the Schrödinger atomic model
- 5 - Advances of Schrödinger's atomic model in relation to other atomic models
Summary about Schrödinger's atomic model
Schrödinger's atomic model is actually the description of the atom and electrons through the Schrödinger equation.
The Schrödinger equation was developed through important studies in the field of quantum mechanics.
The wave-particle duality, the uncertainty principle, among other theories, were essential for the creation of the Schrödinger equation.
Solving the Schrödinger equation, it is possible to describe the energy of the atom as well as that of the electron.
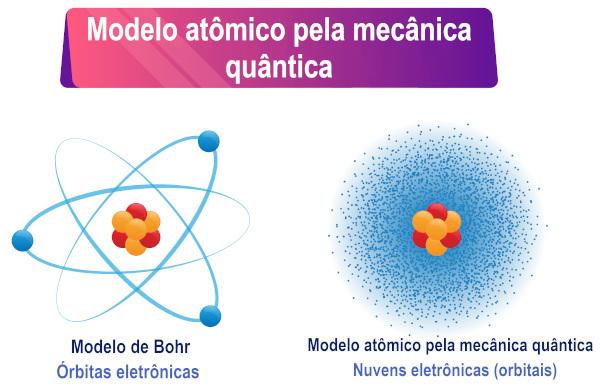
Based on the interpretation of the Schrödinger equation, it can be seen that electrons do not have a definite orbit around the atom, but rather a region of probability of existence around from him.
Schrödinger's studies expand the understanding of the atom proposed by Bohr, as they allow an understanding of the behavior of polyelectronic atoms.
What is Schrödinger's atomic model?
The Schrödinger atomic model is a common name for the description of an atomic model based on quantum mechanics. The main characteristic of this model is the mathematical interpretation of the wave-particle duality adopted by electrons, more specifically, the replacement of a well-defined trajectory of the electron by the probability of existence of the electron around the core.
Such an interpretation began through the work of the Austrian scientist Erwin Schrödinger, in 1927, after important advances in understanding matter in the field of quantum mechanics, such as the photoelectric effect, the uncertainty principle and duality wave-particle.
The understanding of Schrödinger's atomic model is not trivial, being approached in more advanced levels of the study of Chemistry.
Do not stop now... There's more after the publicity ;)
Experimental basis for Schrödinger's atomic model
Before the studies of Erwin Schrödinger, there were important advances in the understanding of matter at the beginning of the 20th century. Such experiments initiated the field of theoretical knowledge known as quantum mechanics, which brings interpretations about the behavior of particles close to or below the atomic scale. In this specific universe, the laws of classical physics, also known as Newtonian physics, often do not apply or are not sufficient to explain certain behaviors.
Just to get an idea, we can say that quantum mechanics starts with a topic known as the ultraviolet catastrophe. According to classical physics, a black body (hot object), with a temperature different from zero, emits intense ultraviolet radiation, in addition to gamma radiation and X-rays.
This means that we human beings, with our temperature of 36-37 °C, would glow in the dark (consequence of incandescence). Needless to say, this is complete nonsense, for if it were, there would be no darkness.
In this context, In 1900, Max Planck created the concept of the how much, translated as “packets of energy”, in order to explain the exchange of energy between matter and radiation. According to his interpretation, a body at low temperatures (like us) does not have enough energy to emit high-frequency ultraviolet radiation.
Thus, a body can only emit high-frequency ultraviolet radiation when it acquires the minimum necessary energy. In this condition, the exchange of energy between matter and surroundings occurs through packets of radiation energy.
Energy packets also bring a difference in relation to classical physics. When talking about packets of energy, it refers to energy that is quantized, that is, it is specific, there is an imposition of limits. In Newtonian physics, the amount of energy exchanged between two objects has no restrictions.
Photoelectric effect
To give robustness to the theories proposed by Planck, more evidence was needed. In this context, the photoelectric effect appeared., which deals with the ejection of electrons from a metal through the incidence of ultraviolet radiation on its surface.
According to the observations of this theory, no electrons are ejected until the radiation reaches a frequency of a certain value, specific for each metal. Once this frequency is reached, the electrons are immediately ejected, and the more intense the frequency of the incident radiation, the faster the ejected electron will have.
A explanation for the photoelectric effect was given by Albert Einstein. According to Einstein, electromagnetic radiation (light, for example, is electromagnetic radiation), used for the ejection of electrons, was composed of particles known as photons, and, moreover, each photon could be interpreted as a packet of energy. Based on Planck's studies, it was possible to conclude that photons of ultraviolet radiation are more energetic than photons of visible light.

When colliding with the surface of the metal, the photons (constituents of electromagnetic radiation) exchange energy with the electrons present there. If the energy absorbed by the electron from colliding with the photons is large enough, then it will be ejected. To learn more about the photoelectric effect, click here.
wave-particle duality
The photoelectric effect brought a strong foundation that electromagnetic radiation is composed of particles (photons). However, many other experiments indicated that electromagnetic radiation behaved like a wave. Of these experiments, the most striking was diffraction — the physical phenomenon observed when a wave encounters an obstacle or, by another interpretation, the ability of waves to overcome obstacles.
O The wave character of light has been known since 1801, when the English physicist Thomas Young shone light on a barrier with a slit. When it passes through this slit, light undergoes diffraction. At each slit, including, that the light passes, even diffracted, it undergoes a new diffraction.

Like this, it was necessary to accept a new behavior for electromagnetic radiation: the wave-particle duality. From there, the French scientist Louis de Broglie expanded this concept, suggesting that all particles should also be understood as having wave behavior.
The de Broglie hypothesis gained strength in 1925, when American scientists Clinton Davisson and Lester Germer proved that an electron beam was capable of undergoing diffraction when passing through a single crystal of nickel.
This perception was essential for arriving at the conclusion that heavier particles, such as molecules, were also capable of undergoing diffraction and, therefore, exhibiting wavelike behavior. To learn more about wave-particle duality, click here.
uncertainty principle
In classical physics, it is easy for you to determine the path of a particle. However, in the quantum world, in which particles also behave like waves, their trajectory is no longer so precise. This because it makes no sense to talk about the location of a wave.
For example, on a guitar, when you pluck a string, the wave spreads out over its entire length. If a particle has this same behavior, there is no way to define its location exactly, even knowing its linear momentum (quantity that mixes mass and velocity).
Therefore, the electron, which also has a dual character, does not have a defined orbit/path around the atomic nucleus, as many believe. Aduality then creates uncertainty about the exact position of the particle.
This uncertainty in the definition of position is negligible for very heavy bodies, but fully significant for bodies of atomic size or subatomic, that is, if you know that the particle is in a certain place, at a certain moment, you will no longer know where it will be in the next instant.
From this dilemma arose the uncertainty principle., established by the German physicist Werner Heisenberg in 1927. According to this principle, it is not possible to know the position and linear momentum of a particle without a margin of error, that is, if one property is known, the other is not. To learn more about the uncertainty principle, click here.
Features of Schrödinger's atomic model
As, from the dual character of the particle, it was no longer possible to define a specific trajectory for it, in 1927, the Austrian scientist Erwin Schrödinger replaced this precise trajectory with a wave function, represented by the Greek letter psi (ψ), with the values of this function varying according to the position. An example of a wave function is the sine function of x.
Scientist Max Born then created a physical interpretation for the wave function, stating that the square of the function ψ, that is, ψ², would be proportional to the probability of finding a particle in a region. Thus, ψ² is understood as the probability density of finding a particle in some region. As it is a probability density, the value of ψ² must be multiplied by the volume to obtain the true probability.
To calculate the wave function, Schrödinger developed an equation, simplified as follows:
Hψ = Eψ
Hψ should be read as “Hamiltonian of psi”, and describes the curvature of the wave function. The Hamiltonian is a mathematical operator, just like the plus, minus, log, etc. The right side brings us the corresponding energy.
The solution of this equation brings us an important conclusion: particles can only have discrete energiess, that is, well-determined energies, or quantized, and not any value. These specific energy values are known as energy levels. This is an imposition of the wave function, as it needs to fit in a specific region of space. In classical mechanics, an object can have any value of total energy.
Like this, an electron cannot have any energy, but well defined energy levels. Since the wave function needs to fit a region of space, remember that a electron is confined inside an atom through the forces of attraction that it has for the nucleus.
The energy levels of an atom can be calculated by appropriately solving the Schrödinger equation. In this case, it is noticed that the resolution reaches a new equation, which demonstrates that the energy of each level in the atom depends on an integer number, called n, which corroborates the idea that energy levels have specific values.
Thus, assigning positive values to n (1, 2, 3...), it is possible to calculate the energy of the atomic levels. The parameter n is now called the principal quantum number, as it ends up linked to each atomic level allowed for an atom.
To the electron wave functions are called atomic orbitals, whose mathematical expressions are also obtained by solving the Schrödinger equation. An atomic orbital presents the distribution of the electron in an atom, that is, the region of probability of existence of an electron in an atom. Atomic orbitals can have different shapes and energies, also obtained by the Schrödinger equation.
For every energy level n (Remembering that n can be 1, 2, 3...), there are n sublevels. In each sublevel, there are orbitals of different shapes. There is no limit to the different orbitals, but with the atoms known so far, chemists use only four of them, identified by the letters s, P, d It is f.
So, for example, at the level n = 1, there is only one sublevel, so there is only the orbital s. Now for the level n = 2, there are two sublevels, the orbitals being present s It is P.

Advances of Schrödinger's atomic model in relation to other atomic models
As mentioned, Schrödinger did not necessarily present a model but a mathematical interpretation. for observed phenomena concerning the nature of particles. Therefore, its interpretation becomes complex, since the Schrödinger equation itself needs advanced mathematical knowledge for its resolution and even for its interpretation.
However, the Schrödinger's studies brought great robustness to justify the energy of atoms and electrons gifts. For example, the resolution of the Schrödinger equation confirms Bohr's atomic model for the hydrogen atom and other hydrogenoid atoms (those that only have 1 electron). Like Schrödinger, Bohr arrived at the permissible energy levels for the hydrogen atom.
However, Bohr's atomic model is not able to reach electronic levels for atoms with more than 1 electron and, thus, demonstrates its main weakness. When two electrons are present, it is necessary to consider the electronic repulsion between them, a parameter that can be added to the mathematical understanding proposed by Schrödinger.
Another important point of Schrödinger's studies is the adaptation of quantum concepts, such as the duality of the particle, as well as an exact trajectory for an electron. The definition of atomic orbital is very important for understanding the structure of all atoms. A probability density (ψ²) helps us understand how electrons occupy atomic orbitals in polyelectronic atoms, bringing more specific information about the energy of the electron.
By Stefano Araujo Novais
Chemistry teacher
Learn more about the structure of the atom and its main constituent particles: protons, neutrons and electrons.
Know the evolution of the atomic model in history.
Click and learn about the main features of Rutherford's atomic model and the experiment that enabled its formulation.
Find out what are the main characteristics, problems and from which aspects Thomson's atomic model was proposed!
Enter and meet the Bohr atom, which was an atomic model based on postulates that successfully described the hydrogen atom.


