O apothem of a polygon is a segment with endpoints at the center of the polygon and at the midpoint of one of the sides. This segment forms a 90° angle with the respective side of the polygon.
To calculate the measure of the apothem, it is necessary to consider the characteristics of the polygon in question. Depending on the geometric shape, it is possible to construct a formula to obtain this measurement. An important observation is that the measure of the apothem of a regular polygon is equal to the measure of the radius of the circumference inscribed in the polygon.
Read too: What is the bisector?
Summary about the apothem
The apothem is the segment of a polygon that connects the center (meeting point of perpendicular bisectors) to the midpoint of one of the sides.
The angle between the apothem and the respective side of the polygon measures 90°.
The measure of the apothem of a regular polygon is equal to the measure of the radius of the circle inscribed in the polygon.
The apothem OM of an equilateral triangle of side l is given by the formula
\(OM = \frac{l\sqrt3}6\)
The apothem OM of a square of side l is given by the formula
\(OM = \frac{l}2\)
The apothem OM of a regular hexagon on one side l is given by the formula
\(OM = \frac{l\sqrt3}2\)
The apothem of a pyramid is the segment that joins the vertex to the midpoint of one of the edges of the base, and its measure can be obtained by the Pythagorean theorem.
Examples of apothem
To find the apothem of a polygon, we must construct the line segment joining the center of the polygon with the midpoint of one of the sides. Remember that the center of a polygon is where the bisectors meet.

In these examples, the apothem was considered in plane polygons. However, there is a space object that has a different kind of apotheme: the pyramid.
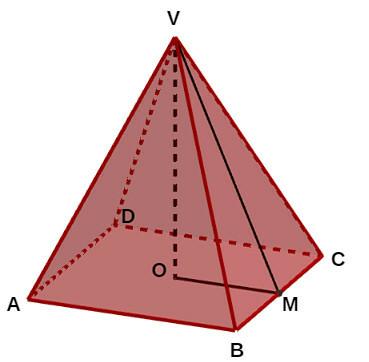
In a pyramid, there are two types of apothem: the apothem of the base, which is the apothem of the polygon that forms the base of the pyramid, and the apothem of the pyramid, which is the segment joining the vertex to the midpoint of a base edge (that is, it is the height of a side face of the base). pyramid).
In the square base example below, segment OM is the apothem of the base and segment VM is the apothem of the pyramid, with M being the midpoint of BC.
What are the formulas for the apothem?
Knowing the characteristics of a polygon, especially regular polygons, we can develop formulas for calculating the measure of the apothem. Let's see what these formulas are for the main regular polygons.
Equilateral triangle apothem formula
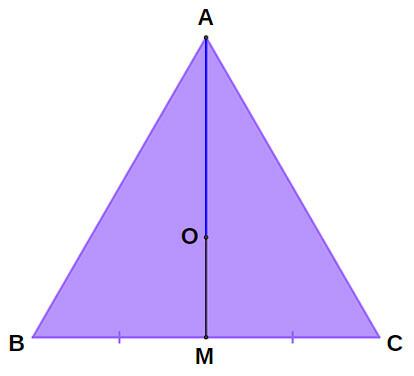
At the equilateral triangle case, the height and median relative to a given side are the same. This means that the center of the polygon coincides with the barycenter of the triangle. Thus, the point O divides the height AM as follows:
\(AO = \frac{2}3 AM\) It is \(OM=\frac{1}3 AM\)
Remember that the measure of height of an equilateral triangle l is given by:
\(Height\ triangle\ equilateral=\frac{l\sqrt3}2\)
Therefore, as AM is the height of the equilateral triangle ABC and the segment OM is the apothem of the triangle, we can elaborate the following expression for the measure of OM, considering that the side of the triangle measures l:
\(OM =\frac{1}3 AM = \frac{1}3 ⋅\frac{l\sqrt3}2\)
\(OM = \frac{l\sqrt3}6\)
Apothem of the Square Formula
In the case of the square, the measure of the apothem corresponds to half the length of the side. Thus, if O is the center of the square, M is the midpoint of one of the sides, and l is the length of the side of the square, so the formula for the apothem OM is
\(OM=\frac{l}2\)
Regular hexagon apothem formula
In the regular hexagon, the apothem corresponds to the height of an equilateral triangle with vertices at two ends of one of the sides and at the center of the polygon. In the example below, the apothem OM of the regular hexagon is the height of the equilateral triangle OCD, where M is the midpoint of CD.
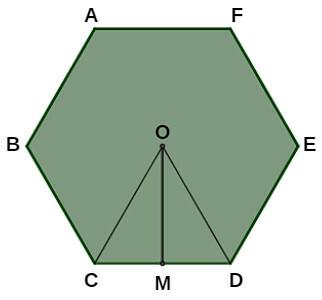
As we mentioned before, the altitude of an equilateral triangle is known. Thus, if the side of a regular hexagon measures l, then the formula for the apothem OM is
\(OM =\frac{l\sqrt3}2\)
Pyramid Apothem Formula
The measure of the apothem of the pyramid can be obtained with the Pythagorean theorem help. In the example below, in a square pyramid, the triangle VOM is a rectangle, with legs VO and OM and hypotenuse VM. Note that VO is the height of the pyramid, OM is the apothem of the base and VM is the apothem of the pyramid.
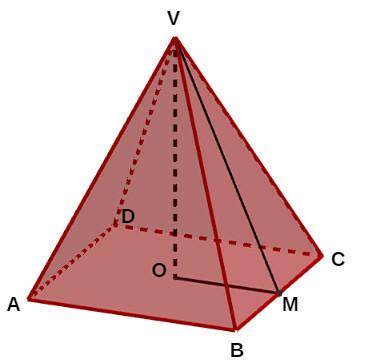
Thus, to determine the measure of the apothem of the pyramid, we must apply the Pythagorean theorem:
\((VM)^2=(VO)^2+(OM)^2\)
Careful! VM is the height of an isosceles triangle, not an equilateral triangle. So, in this case, we cannot use the formula for the height of an equilateral triangle.
How is the apothem calculated?
To calculate the apothem of a polygon or the pyramid, we can use the constructed formulas or associate the apothem with the radius of the inscribed circle.
Example 1: Assume that a circle of radius 3 cm is inscribed in an equilateral triangle. What is the measure of the apothem of this triangle?
As the apothem of a polygon has the same measure as the radius of the inscribed circle, the apothem of the triangle measures 3 cm.
Example 2: What is the measure of the apothem of a regular hexagon with a side of 4 cm?
Using the formula for the apothem of a regular hexagon with \(l=4\) cm, we have to
\(Measurement\ of\ apothem=\frac{4\sqrt3}2=2\sqrt3\ cm\)
Read too: All about the notable points of a triangle
Solved exercises on the apothem
question 1
If a pyramid 4 cm high has a base apothem of 3 cm, then the measurement of the apothem of the pyramid is
a) 5 cm
b) 6 cm
c) 7 cm
d) 8 cm
e) 9 cm
Resolution:
In a pyramid, we can construct a right triangle in which one leg is the apothem of the base, the other leg is the height of the pyramid and the hypotenuse is the apothem of the pyramid. Thus, applying the Pythagorean theorem to the hypotenuse of measure x,
\(x^2=3^2+4^2\)
\(x = 5\ cm\)
Alternative A.
question 2
If the apothem of a square is y cm, then the side of the square is
The) \(\frac{1}3y \) cm
B) \(\frac{1}2y \) cm
c) y cm
d) 2y cm
e) 3y cm
Resolution
The apothem of a square is half the length of the side of the square. Therefore, if the apothem measures y cm, the square measures 2y cm.
Alternative D.
By Maria Luiza Alves Rizzo
Math teacher