bisector and the perpendicular line to a segment that intersects its midpoint. We can construct the perpendicular bisector of a segment using ruler and compass. On a triangle, the bisectors are lines perpendicular to the sides that contain their midpoints. Thus, a triangle has three perpendicular bisectors. The point where these bisectors meet is called the circumcenter and constitutes the center of the circle circumscribed to the triangle.
Read too: Distance between two points — the shortest path between two points in the Cartesian plane
Topics of this article
- 1 - Summary about bisector
- 2 - What is a bisector?
- 3 - How to build the perpendicular bisector?
- 4 - How to find the bisector equation?
- 5 - Bisector of a triangle
- 6 - Differences between bisector, median, bisector and height of a triangle
- 7 - Solved exercises on bisector
Bisector is the straight perpendicular to a segment passing through the midpoint.
The points of a perpendicular bisector are equidistant from the endpoints of the segment.
The perpendicular bisector can be constructed with ruler and compass.
The equation of a perpendicular bisector can be determined based on the coordinates of the endpoints of the segment.
A triangle has three perpendicular bisectors, one with respect to each side.
The intersection point of the bisectors of a triangle is called the circumcenter. This point is the center of the circumscribed circle of the triangle.
The bisector of a triangle differs from the median, the bisector and the height of a triangle.
Do not stop now... There's more after the publicity ;)
Given a segment, the perpendicular bisector is the line perpendicular to the segment that intercepts your midpoint.
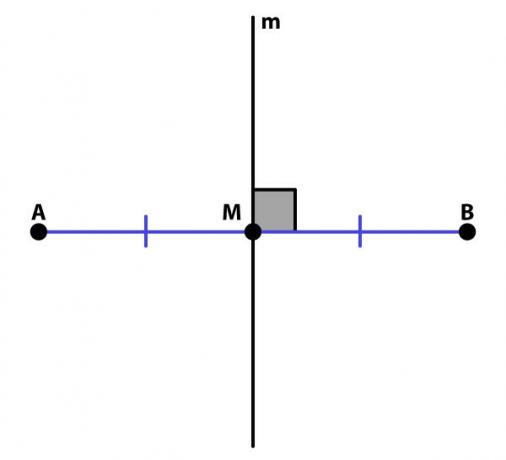
An important consequence of this definition is that all points on a perpendicular bisector are the same distance from the endpoints of the segment. In mathematical symbology, if AB is a segment and the point P belongs to the bisector, then PA = PB.
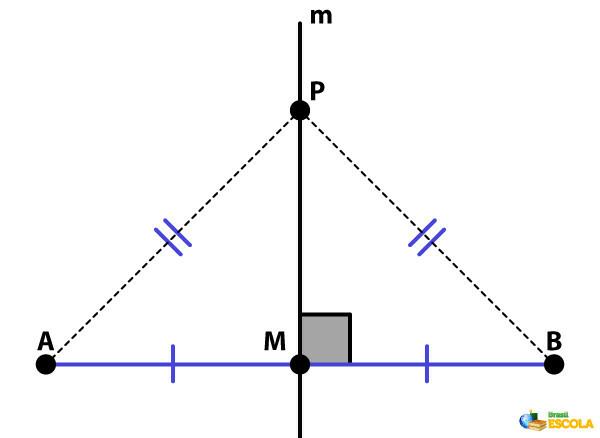
To construct the perpendicular bisector of a segment, we only need ruler and compass. The steps for construction are as follows:
Step 1: Given a segment AB, open the compass with a length greater than half the segment. Hint: one possibility is to use the length of the segment itself.
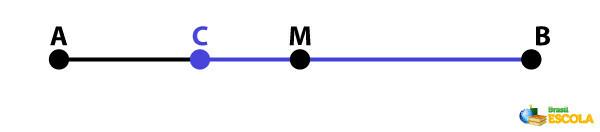
Step 2: draw one circumference with center at one end of the segment and radius with the measure chosen in step 1.

Step 3: Repeat step 2 for the other end of the segment.

Step 4: Join the intersection points of the circles with the ruler.

Since the perpendicular bisector is a straight line, we can determine a equation that describes your points, being r the line that contains a segment AB given away, s the bisector of this segment and P (x, y) any point on the perpendicular bisector.
Assuming that the coordinates of the points A It is B are known, we can obtain the angular coefficient n of the straight r. As r It is s are perpendicular, the slope m of the straight s (the perpendicular bisector) can also be found, as it is the opposite of the multiplicative inverse of n. Using the expression for the fundamental equation of the line, \(y-y_0=m (x-x_0 )\), on what \(M(x\_0,y\_0)\) is the midpoint of AB, we have completed the bisector equation.
Example:
Determine the bisector equation of the segment determined by the points A(1,2) and B(3,6).
Resolution:
First, let's get the slope n of the straight r that contains the segment AB:
\(n_r=\frac{Δ y}{Δ x}=\frac{6-2}{3-1}=\frac{4}2 =2\)
Now we look for the midpoint M of the segment AB:
\(M(x_0,y_0 )=M(\frac{1+3}{2},\frac{2+6}{2})=M(2,4)\)
Remember that the perpendicular bisector s wanted is perpendicular to the line r (which contains the segment AB). Then, the angular coefficient m of the straight s and the angular coefficient n of the straight r are related as follows:
\(m_s=\frac{-1}{n_r} \)
Therefore, \( m_s=\frac{-1}2\).
Finally, we use the fundamental equation of the line to determine the bisector s, a line that has slope equal to \(-\frac{1}2\) and passes through the point (2,4):
\(y-y_0=m\cdot (x-x_0 )\)
\(y-4=-\frac{1}2\cdot (x-2)\)
\(y=-\frac{1}2 x+5\)
The three sides of a triangle are line segments. Thus, the term “bisector of a triangle” refers to the bisector of one of the sides of this geometric figure. Therefore, the trianglehas three bisectors. See below:

The point where the bisectors of a triangle meet is called the circumcenter., since it is the center of the circle circumscribed to the triangle (that is, the circle that passes through the three vertices of the triangle).

Important:As the circumcenter is a point common to the three perpendicular bisectors, its distance from each of the vertices is the same. In mathematical symbology, if D is the circumcenter of the triangle ABC, then \(AD=BD=CD\).
Bisector, median, bisector and height of a triangle are different concepts. Let's look at each individually and then together.
Bisector of a triangle: is the line perpendicular to one of the sides that intersects its midpoint.
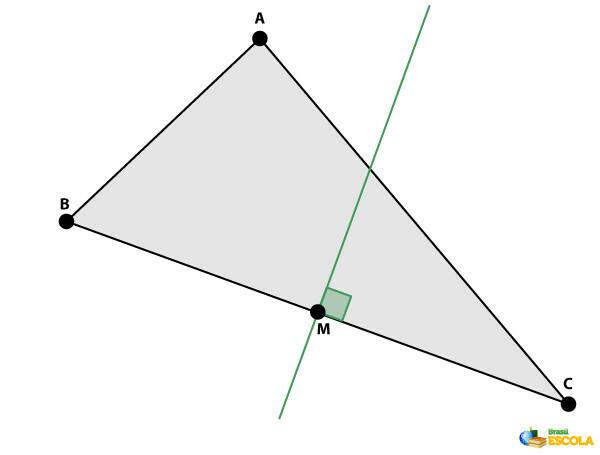
Median of a triangle: is the segment with endpoints at a vertex of the triangle and at the midpoint of the side opposite the vertex.
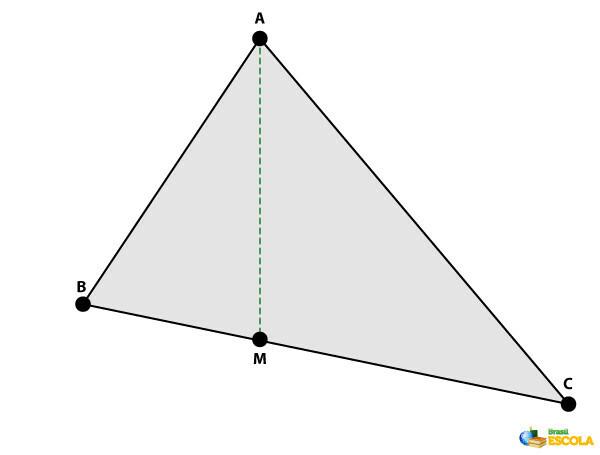
Bisector of a triangle: is the segment that divides in half one of the angles sides of the triangle, with endpoints at one of the vertices and on the opposite side.
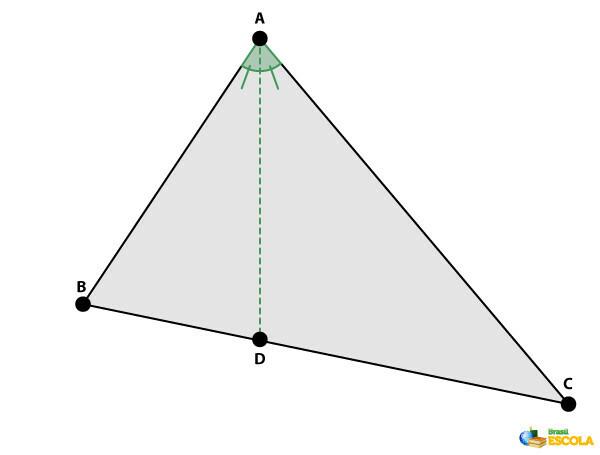
Height of a triangle: is the segment perpendicular to one of the sides with end at the angle opposite the side.

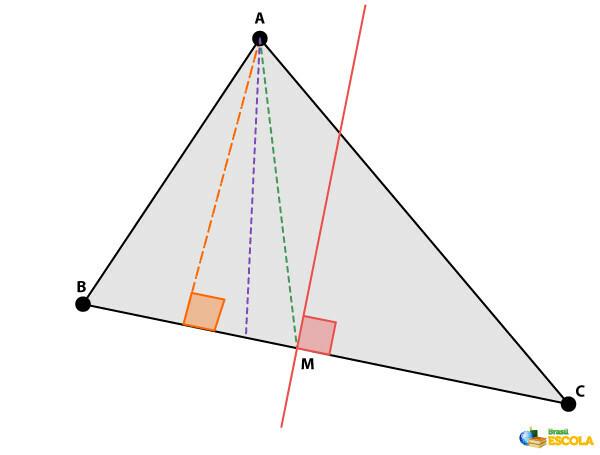
In the following image, we highlight, in relation to the segment BC of the triangle, the height (dotted line dash in orange), the bisector (dashed line in purple), the median (dotted line in green) and the perpendicular bisector (solid line in red).
Important: On a equilateral triangle, that is, which has the three sides and three angles equal, the bisectors, medians, bisectors and heights coincide. Consequently, the notable points of a triangle (circumcenter, barycenter, incenter and orthocenter) also coincide. In the image below, we highlight, in relation to segment BC, the bisector, median, bisector and height in a continuous black line. The highlighted point E is therefore the circumcenter, barycenter, incenter and orthocenter of the triangle ABC.

See too: Metric relations in the inscribed equilateral triangle — what are they?
question 1
Consider the following statements.
i. The bisector of a triangle is the segment that starts at a vertex and crosses the midpoint of the opposite side.
II. The point where the bisectors of a triangle meet is called the circumcenter. This point is the center of the circle circumscribed to the triangle and equidistant from the vertices.
III. The bisector of a segment is the perpendicular line that intersects the segment at the midpoint.
Which alternative contains the correct one(s)?
A) I, only.
B) II, only.
C) III, only.
D) I and II.
E) II and III.
Resolution:
Alternative E
Statement I is the only incorrect one, as it describes the median of a triangle.
question 2
(Enem — adapted) In recent years, television has undergone a real revolution in terms of image quality, sound and interactivity with the viewer. This transformation is due to the conversion of the analog signal to the digital signal. However, many cities still do not have this new technology. Seeking to bring these benefits to three cities, a television station intends to build a new transmission tower that sends a signal to antennas A, B and C, already existing in these cities. The antenna locations are represented in the Cartesian plane:

The tower must be located equidistant from the three antennas. The suitable place for the construction of this tower corresponds to the point of coordinates
A) (65, 35).
B) (53, 30).
C) (45, 35).
D) (50, 20).
E) (50, 30).
Resolution:
Alternative E
Note that the location for the tower must be the circumcenter of the triangle formed by points A, B and C, as it is the equidistant location of the three antennas.
The coordinates for the T tower are\( (x_t, y_t )\). Since T belongs to the bisector of AB (given by the line x = 50), the horizontal location of the tower must be \(x_t=50\).
To determine the horizontal coordinate \(y_t\) of the tower, we can use the expression for the distance between two points twice. As the tower is equidistant, for example, from vertices A and C (AT = CT), we have:
\(\sqrt{(30-50)^2+(20-y_t )^2}=\sqrt{(60-50)^2+(50-y_t )^2}\)
Simplifying, we get \(y_t=30\).
By Maria Luiza Alves Rizzo
Math teacher
Find out what the apothem of a polygon is and how to calculate its measure. Also know the main formulas for this calculation.
See here the main characteristics of the circumference and learn how to calculate its area and length. See also how to write the equation of a circle.
Determining the tangent of the angle of inclination of the line.
The shortest distance between any two points is a straight line. See how to calculate this distance and learn how to establish a mathematical relationship to determine it
Find out what the general equation of the line is and how to find it, in addition to checking the graphical representation of a line from its equation.
Learn how to calculate the midpoint of a line segment using Analytical Geometry!
See here the notable points of a triangle and learn its main properties. See also how these points can facilitate the resolution of some problems.
Understand what perpendicular lines are and learn what is the condition for two lines represented in the Cartesian Plane to be perpendicular or not.