A diamond area is the measurement of its inner region. One way to calculate the area of a rhombus is to determine the half of the product between the larger diagonal and the smaller diagonal, whose measures are represented by D It is d respectively.
Read too: How to calculate the area of a square?
Topics of this article
- 1 - Summary about the area of the rhombus
- 2 - Elements of the rhombus
- 3 - Properties of the diagonals of the rhombus
- 4 - Formula for the area of the rhombus
- 5 - How to calculate the area of a rhombus?
- 6 - Exercises on the area of the rhombus
Summary about the area of the rhombus
A rhombus is a parallelogram with four congruent sides and opposite congruent angles.
The two diagonals of a rhombus are known as the larger diagonal (D) and smaller diagonal (d).
Each diagonal of a rhombus divides that polygon into two congruent triangles.
The two diagonals of the rhombus are perpendicular and intersect at their midpoints.
The formula for calculating the area of the rhombus is:
\(A=\frac{D\times d}{2}\)
Do not stop now... There's more after the publicity ;)
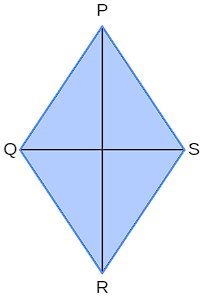
rhombus elements
the diamond is a parallelogram formed by four sides of equal length and opposite angles of the same measure. In the diamond below, we have \(\overline{PQ}=\overline{QR}=\overline{RS}=\overline{SP}\), \(\hat{P}=\hat{R}\) It is \(\hat{Q}=\hat{S}\).

The segments with ends at opposite vertices are the diagonals of the rhombus. In the image below, we call the segment \(\overline{PR}\) in larger diagonal and the segment \(\overline{QS}\) in smaller diagonal.
Diagonal properties of the rhombus
Let's know two properties related to the diagonals of the rhombus.
Property 1: Each diagonal divides the rhombus into two congruent isosceles triangles.
First consider the larger diagonal \(\overline{PR}\) of a rhombus PQRS beside l.
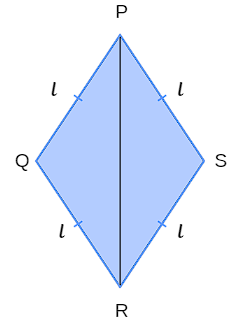
realize that \(\overline{PR}\) Divide the rhombus into two triangles: PQR It is PSR. Yet:
\(\overline{PQ}=\overline{PS}=l\)
\(\overline{QR}=\overline{SR}=l\)
\(\overline{PR}\) it's common side.
Thus, by the LLL criterion, the triangles PQR It is PSR are congruent.
Now consider the smaller diagonal \(\overline{QS}\).

realize that \(\overline{QS} \) Divide the rhombus into two triangles: PQS It is RQS. Yet:
\(\overline{PQ}=\overline{RQ}=l\)
\(\overline{PS}=\overline{RS}=l\)
\(\overline{QS}\) it's common side.
Thus, by the LLL criterion, the triangles PQS It is RQS are congruent.
Property 2: The diagonals of a rhombus are perpendicular and intersect at the midpoint of each other.
The angle formed by the diagonals \(\overline{PR}\) It is \(\overline{QS}\) measures 90°.
It isO the meeting point of the diagonals \(\overline{{PR}}\) It is \(\overline{{QS}}\); like this, O is midpoint of \(\overline{PR}\) and is also the midpoint of \(\overline{QS}\). if \( \overline{PR}\)give me D It is \(\overline{QS}\) give me d, This means that:
\(\overline{PO}=\overline{OR}=\frac{D}{2}\)
\(\overline{QO}=\overline{OS}=\frac{d}{2}\)

Observation: The two diagonals of a rhombus divide this figure into four congruent right triangles. consider the triangles PQO, RQO, PSO It is RSO. Note that each has a measurement side. l (the hypotenuse), one of measure \(\frac{D}{2}\) and another measure \(\frac{d}{2}\).
See too: Comparison and similarity between triangles
rhombus area formula
It is D the length of the larger diagonal and d the measure of the smaller diagonal of a rhombus; The formula for the area of the rhombus is:
\(A=\frac{D\times d}{2}\)
Below is a demonstration of this formula.
According to the first property we study in this text, the diagonal \(\overline{QS}\) divide the diamond PQRS into two congruent triangles (PQS It is RQS). This means that these two triangles have the same area. Consequently, the area of the rhombus is twice the area of one of these triangles.
\(A_{\mathrm{diamond}}=2\times A_{triangle} PQS\)
According to the second property we studied, the base of the triangle PQS give me d and the height measures D2. Remember that the area of a triangle can be calculated by base×height2. Soon:
\(A_{\mathrm{diamond}}=2\times A_{triangle} PQS\)
\(A_{\mathrm{diamond}}=2\times\left(\frac{d\times\frac{D}{2}}{2}\right)\)
\(A_{\mathrm{diamond}}=2\times\left(\frac{d\times\frac{D}{2}}{2}\right)\)
\(A_{\mathrm{diamond}}=\frac{D\times d}{2}\)
How to calculate the area of a rhombus?
As we saw, if the measures of the diagonals are informed, it is enough apply the formula to calculate the area of a rhombus:
\(A=\frac{D\times d}{2}\)
Otherwise, we need to adopt other strategies, considering, for example, the properties of this polygon.
Example 1: What is the area of a rhombus whose diagonals measure 2 cm and 3 cm?
Applying the formula, we have:
\(A_{\mathrm{diamond}}=\frac{D\times d}{2}\)
\(A_{\mathrm{diamond}}=\frac{3\times2}{2}\)
\(A_{\mathrm{diamond}}=3 cm²\)
Example 2: What is the area of a rhombus whose side and smaller diagonal measure, respectively, 13 cm and 4 cm?
By observing property 2, the diagonals of a rhombus divide this polygon into four right triangles congruent. Each right triangle has legs of measure \(\frac{d}{2}\) It is \(\frac{D}{2}\) and measure hypotenuse l. By the Pythagorean theorem:
\(l^2=\left(\frac{d}{2}\right)^2+\left(\frac{D}{2}\right)^2\)
replacing \(d=4 cm\) It is d=4 cm, we have to
\(\left(\sqrt{13}\right)^2=\left(\frac{4}{2}\right)^2+\left(\frac{D}{2}\right)^2\ )
\(13=4+\frac{D^2}{4}\)
\(D^2=36\)
As D is the measure of a segment, we can only consider the positive result. I.e:
D=6
Applying the formula, we have:
\(A_{\mathrm{diamond}}=\frac{D\times d}{2}\)
\(A_{\mathrm{diamond}}=\frac{6\times4}{2}\)
\(A_{\mathrm{diamond}}=\ 12 cm²\)
Know more: Formulas used to calculate the area of plane figures
Exercises on the area of the rhombus
question 1
(Fauel) In a rhombus, the diagonals measure 13 and 16 cm. What is the measurement of your area?
a) 52 cm²
b) 58 cm²
c) 104 cm²
d) 208 cm²
e) 580 cm²
Resolution: alternative C
Applying the formula, we have:
\(A_{\mathrm{diamond}}=\frac{D\times d}{2}\)
\(A_{\mathrm{diamond}}=\frac{16\times13}{2}\)
\(A_{\mathrm{diamond}}=\ 104 cm²\)
question 2
(Fepese) A factory produces ceramic pieces in the shape of a diamond, whose smaller diagonal measures a quarter of the larger diagonal and the larger diagonal measures 84 cm.
Therefore, the area of each ceramic piece produced by this factory, in square meters, is:
a) greater than 0.5.
b) greater than 0.2 and less than 0.5.
c) greater than 0.09 and less than 0.2.
d) greater than 0.07 and less than 0.09.
e) less than 0.07.
Resolution: alternative D
if D is the larger diagonal and d is the smaller diagonal, then:
\(d=\frac{1}{4}D\)
\(d=\frac{1}{4}\cdot84\)
\(d=21 cm\)
Applying the formula, we have
\(A_{\mathrm{diamond}}=\frac{D\times d}{2}\)
\(A_{\mathrm{diamond}}=\frac{84\times21}{2}\)
\(A_{\mathrm{diamond}}=882 cm²\)
As 1 cm² corresponds to \(1\cdot{10}^{-4} m²\), then:
\(\frac{1\ cm^2}{882\ cm^2}=\frac{1\cdot{10}^{-4}\ m^2}{x}\)
\(x=0.0882 m²\)
By Maria Luiza Alves Rizzo
Math teacher
Would you like to reference this text in a school or academic work? Look:
RIZZO, Maria Luiza Alves. "Area of the rhombus"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/area-do-losango.htm. Accessed May 12, 2023.
Learn the definition of a parallelogram and its properties, as well as learn about the main parallelograms and their formulas for area and perimeter.
Learn what polygons are and what their elements are. Know the method of naming polygons and how we add the internal and external angles.
Get to know quadrilaterals and the basic characteristics that lead them to be classified as parallelograms, trapezoids or neither.
Check out the cases in which it is possible to check the similarity of triangles without the need to measure all their sides and angles.
The Pythagorean theorem is one of the most important tools in the study of triangles. Click here, learn about its formula and find out how to apply it!
Understand what a triangle is, as well as learn how to calculate its area and perimeter. See also the types of this figure and learn to identify each one of them.
Learn to calculate the area of a plane figure. Know the area formulas of the main flat figures, such as the square, rectangle, triangle, circle, rhombus and trapeze.
Click here, learn how to calculate the area of the triangle and know the specific formulas to perform this calculation according to each case.


