A area of right triangle is the measure of its surface. This area, like that of any triangle, is half the product of the base and height. As the legs of a right triangle form 90°, it is convenient to consider one of the legs as the base, since the other leg will be the height.
Read too: Area of the pyramid — how to calculate?
Topics of this article
- 1 - Summary on the area of the right triangle
- 2 - What is the formula for the area of a right triangle?
- 3 - How do you calculate the area of a right triangle?
- 4 - Solved exercises on the area of the right triangle
Summary on area of right triangle
O triangle A rectangle has two sides that form 90° to each other (the legs) and a third side opposite the 90° angle (the hypotenuse).
The area of the right triangle is half the product of the base and the height.
If one of the legs is the base of the triangle, the height will be the other leg.
If the base of the triangle is the hypotenuse, the height is the distance between the hypotenuse and the opposite vertex.
Do not stop now... There's more after the publicity ;)
What is the formula for the area of a right triangle?
A area of any triangle is given by half the product of the base and the height:
\(Area\ of\ triangle =\frac{base\cdot height}2\)
Let ABC be a right triangle with W =90°. Note that we can consider the leg BC as the base of the triangle. Consequently, the leg AC will be the height of that triangle. This strategy is a way to easily find the area of a right triangle, assuming its sides are known.
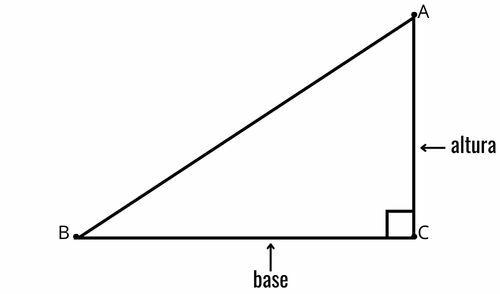
The same reasoning can be done considering the AC leg as the basis, which results in the cathetus BC as height. The formula is applied in the same way.

It is also possible to take hypotenuse AB as the base of the triangle. In that case, the height of the triangle will be the segment with origin at \(\hat{C}\)which forms a right angle with the base at a point D, where h is the measure of the height CD.
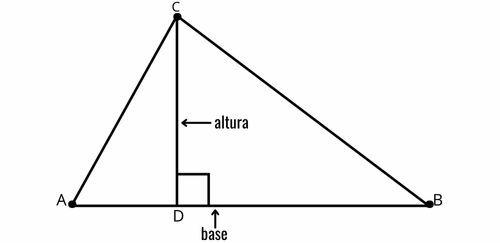
In that case, the height H can be determined through the similarity of triangles between ABC and one of the right triangles formed by CD. consider The as the measure of the side BC, B as the measure of side AC and w as the measure of side AB. The similarity of triangles results in the following relation:
\(h=\frac{a ‧ b}c\)
After obtaining the value of h by this expression, just apply the formula for the area of any triangle.
How do you calculate the area of a right triangle?
To calculate the area of the right triangle, you need to use its formula. See the following example.
Example:
Consider a right triangle with legs measuring 6 cm and 8 cm. Find the area of this triangle.
Resolution:
For simplicity, we can take one of the legs as the basis. So the other leg will be the height.
Taking the 6 cm leg as the base and therefore the 8 cm leg as the height, we have
\(Area\ of\ triangle = \frac{base ‧ height}2=\frac{6 ‧ 8}2 = 24\ cm^2\)
See too: Trapezoid area — how to calculate?
Solved exercises on area of right triangle
question 1
If ABC is a right triangle with legs measuring x cm and (2x - 1) cm and hypotenuse measuring (x + 1) cm, what is the area of this triangle?
Resolution:
Using one of the legs as the base (and therefore the other as the height):
\(Area\ of\ triangle=\frac{base ‧ height}2=\frac{x ‧ (2x-1)}2=\frac{2x^2-x}2=x^2-\frac{x} 2 cm^2\)
question 2
Consider a terrain in the shape of a right triangle. The front of this land corresponds to one of the collarbones and measures 5 meters. Knowing that the distance from the front to the back end of the lot is 12 meters, determine the area of the lot.
Resolution:
One of the collarbones (at the front) measures 5 meters. Note that the distance between the front and the most extreme point of the back (12 meters) corresponds to the other leg and, therefore, indicates the height of the right triangle. Soon:
\(Area\ of\ triangle=\frac{base ‧ height}2=\frac{5 ‧ 12}2=30\ m^2\)
By Maria Luiza Alves Rizzo
Math teacher
Would you like to reference this text in a school or academic work? Look:
RIZZO, Maria Luiza Alves. "Area of right triangle"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/area-do-triangulo-retangulo.htm. Accessed May 15, 2023.
Trigonometric definitions in the right triangle.
Check out the cases in which it is possible to check the similarity of triangles without the need to measure all their sides and angles.
Know what are the particularities of the right triangle and learn to calculate its area and perimeter. See also how trigonometry can be applied to it.


