Let's determine the function that goes through a colon. For this, we need to find the coordinates of these two points, where the y’ coordinate is determined by the value of the function at the x’ coordinate (x1, f (x1)), (x2, f (x2)).
By the definition of an affine function, we have that it is determined by the following expression f (x)=ax+b, that is, to determine such a function, we just need to find the coefficients a, b. We will see that to find these coefficients we only need two points and the value of the function at those points.
Before we show the expression for the general case, let's see how to proceed in an example.
With f(1)=4 and f(2)=6, we then have two points and the function values at these points.
For f (1) we have: f (1) = 4 = a.1+b
For f(2) we have: f(2) = 6 = a.2+b
We will highlight these two relations of equality:
6=2a+b (-), if we subtract one equality from the other, we have the following result:
4=a+b
2=a, that is, a is equal to 2. We find the value of one of the coefficients. To find the other, just replace the result in one of the equals. We will use the second:
4=a+b
as a=2 we have, 4=2+b so we have, b=2
Since f (x)=ax+b and a=2 and b=2, we have that this function, for f (1)=4 and f (2)=6, will be as follows:
f(x)=2x+b.
But this is the process carried out for a specific case. What would the expression look like for us to determine the values of the coefficients of any function? We'll see now.
be y1=f(x1) and y2=f(x2), these points being distinct points. We will have that the expression of these points will be given as follows:
y1=f(x1)=ax1+b
y2=f(x2)=ax2+b, subtract the expression below from the one above. With that, we will have: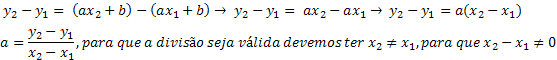
Having the expression for the coefficient The, we will substitute the expression for this coefficient in y1.

In this way, see that the expressions for the coefficients a, b, are determined only by the values of the points, values that we know.
With this, we saw that it is possible to determine an affine function, knowing only the values of two points.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Matrix and determinant - Math- Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/determinando-uma-funcao-afim-pelo-valor-dois-pontos.htm

