O cube, also known as a hexahedron, is a geometric solid which has six faces, all of them made up of squares. In addition to the 6 faces, the cube has 12 edges and 8 vertices. studied in Spatial Geometry, the cube has all its edges congruent and perpendicular, so it is classified as a regular polyhedron. We can perceive the presence of the cube format in our daily lives, in common data used in games, packaging, boxes, among other objects.
Read too: Pyramid — geometric solid that has all its faces formed by triangles
Topics in this article
- 1 - Summary about cube
- 2 - What is a cube?
- 3 - Elements of the cube's composition
- 4 - Cube planning
-
5 - Cube formulas
- Area of the base of a cube
- cube side area
- total cube area
- cube volume
- cube diagonals
- 6 - Exercises solved on cube
cube summary
The cube is also known as a hexahedron, because it has 6 faces.
The cube is composed of 6 faces, 12 edges and 8 vertices.
The cube has all its faces formed by squares, so its edges are congruent, and therefore it is a regular polyhedron, also known as Plato's solid.
The area of the base of the cube is equal to the area of a square. Being The the measure of the edge, to calculate the area of the base, we have that:
\(A_b=a^2\)
The lateral area of the cube is formed by 4 squares of sides measuring The, so to calculate it, we use the formula:
\(A_l=4a^2\)
To calculate the total area of the cube, just add the area of its two bases with the lateral area. So, we use the formula:
\(A_T=6a^2\)
The volume of the cube is calculated by the formula:
\(V=a^3\)
The measure of the side diagonal of the cube is calculated by the formula:
\(b=a\sqrt2\)
The measure of the diagonal of the cube is calculated by the formula:
\(d=a\sqrt3\)
What is cube?
The cube is a geometric solid composed of 12 edges, 8 vertices and 6 faces. Due to the fact that it has 6 faces, the cube is also known as a hexahedron.

Cube Composition Elements
Knowing that the cube has 12 edges, 8 vertices and 6 faces, see the following image.
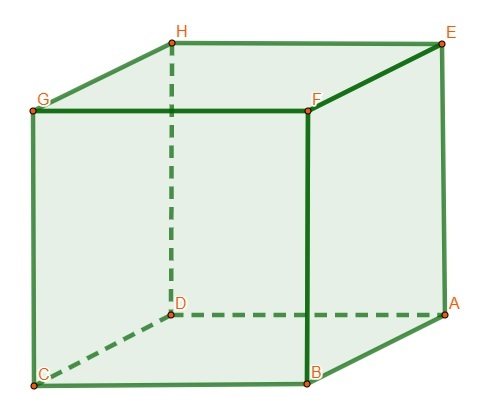
A, B, C, D, E, F, G and H are the vertices of the cube.
\(\overline{AB},\ \overline{AD},\ \overline{AE},\ \overline{BC},\ \overline{BF},\ \overline{CD,\ }\overline{CG}, \ \overline{DH,\ }\overline{HG},\ \overline{EH}\overline{,\ EF},\ \overline{FG}\) are the edges of the cube.
ABCD, ABFE, BCFG, EFGH, ADHE, CDHG are the faces of the cube.
The cube is composed of 6 square faces, so all its edges are congruent. Because its edges have the same measure, the cube is classified as a polyhedron Plato's regular or solid, together with the tetrahedron, octahedron, icosahedron and dodecahedron.
Do not stop now... There's more after the ad ;)
cube planning
To calculate the cube area, it is important to analyze your planning. The cube's unfolding is composed of 6 squares, all congruent with each other:
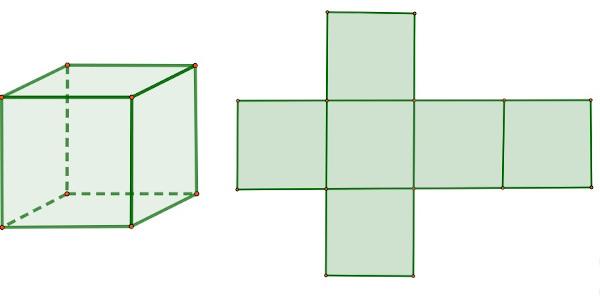
The cube is made up of 2 square bases, and its lateral area is made up of 4 squares, all congruent.
See too: Planning of the main geometric solids
cube formulas
To calculate the base area, side area, total area and volume of the cube, we will consider the cube with edge measuring The.
Area of the base of a cube
As the base is formed by a square of edge The, the area of the base of the cube is calculated by the formula:
\(A_b=a^2\)
Example:
Calculate the measure of the base of a cube that has an edge measuring 12 cm:
Resolution:
\(A_b=a^2\)
\(A_b={12}^2\)
\(A_b=144\ cm^2\)
cube side area
The side area of the cube is made up of 4 squares, all with sides measuring The. Thus, to calculate the lateral area of the cube, the formula is:
\(A_l=4a^2\)
Example:
What is the lateral area of a cube that has an edge measuring 8 cm?
Resolution:
\(A_l=4a^2\)
\(A_l=4\cdot8^2\)
\(A_l=4\cdot64\)
\(A_l=256\ cm^2\)
total cube area
The total area of the cube or simply the area of the cube is the sum area of all cube faces. We know that it has a total of 6 sides, formed by squares of side The, then the total area of the cube is calculated by:
\(A_T=6a^2\)
Example:
What is the total area of a cube whose edge is 5 cm?
Resolution:
\(A_T=6a^2\)
\(A_T=6\cdot5^2\)
\(A_T=6\cdot25\)
\(A_T=150\ cm^2\)
cube volume
The volume of a cube is the multiplication the measure of its three dimensions. As they all have the same measure, we have:
\(V=a^3\)
Example:
What is the volume of a cube that has an edge measuring 7 cm?
Resolution:
\(V=a^3\)
\(V=7^3\)
\(V=343\ cm^3\)
cube diagonals
On the cube we can draw the side diagonal, that is, the diagonal of its face, and the diagonal of the cube.
◦ cube side diagonal
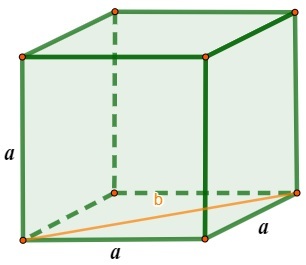
The lateral diagonal or diagonal of a cube face is indicated by the letter B in the image. Fur Pythagorean theorem, we have one right triangle of peccaries measuring The and hypotenuse measuring B:
b² = a² + a²
b² = 2a²
b = \(\sqrt{2a^2}\)
b = \(a\sqrt2\)
Therefore, the formula to calculate the diagonal of a face of the cube is:
\(b=a\sqrt2\)
◦ cube diagonal
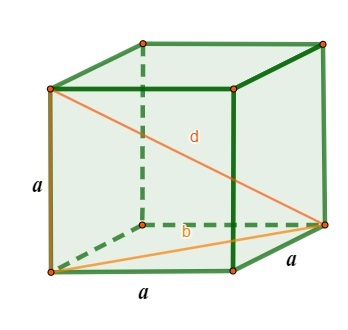
the diagonal d of the cube can be calculated using the Pythagorean theorem as well, since we have a right triangle with legs B, The and hypotenuse measuring d:
\(d^2=a^2+b^2\)
But we know that b =\(a\sqrt2\):
\(d^2=a^2+\left (a\sqrt2\right)^2\)
\(d^2=a^2+a^2\cdot2\)
\(d^2=a^2+2a^2\)
\(d^2=3a^2\)
\(d=\sqrt{3a^2}\)
\(d=a\sqrt3\)
So, to calculate the diagonal of the cube, we use the formula:
\(d=a\sqrt3\)
Know more: Cylinder — a geometric solid that classifies as a round body
Cube solved exercises
question 1
The sum of the edges of a cube is equal to 96 cm, so the measure of the total area of this cube is:
A) 64 cm²
B) 128 cm²
C) 232 cm²
D) 256 cm²
E) 384 cm²
Resolution:
Alternative E
First, we will calculate the measure of the edge of the cube. Since it has 12 edges and we know that the sum of the 12 edges is 96, we have:
The = 96: 12
The = 8 cm
Knowing that each edge measures 8 cm, it is now possible to calculate the total area of the cube:
\(A_T=6a^2\)
\(A_T=6\cdot8^2\)
\(A_T=6\cdot64\)
\(A_T=384\ cm^2\)
question 2
A water tank needs to be emptied for cleaning. Knowing that it has the shape of a cube with an edge of 2 m and that 70% of this reservoir is already empty, then the volume of this reservoir that is still occupied is:
A) 1.7 m³
B) 2.0 m³
C) 2.4 m³
D) 5.6 m³
E) 8.0 m³
Resolution:
Alternative C
First, we will calculate the volume:
\(V=a^3\)
\(V=2^3\)
\(V=8\ m^3\)
If 70% of the volume is empty, then 30% of the volume is occupied. Calculating 30% of 8:
\(0.3\cdot8=2.4\ m^3\)
By Raul Rodrigues de Oliveira
Maths teacher
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Raul Rodrigues de. "Cube"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/cubo.htm. Accessed on July 23, 2022.

