THE Ohm's first law postulates that if in a electric circuit composed of a resistor, without temperature variation, we connect an electric voltage, the resistor will be crossed by an electric current. Through it, we perceive the proportionality relationship between voltage, resistance and electric current, and if we increase the value of one of these quantities, the others will also be affected.
Know more: What is the speed of electric current?
Topics in this article
- 1 - Summary of Ohm's first law
- 2 - Video lesson on Ohm's first law
- 3 - What does Ohm's first law say?
- 4 - What are resistors?
- 5 - What is electrical resistance?
- 6 - Ohm's first law formula
-
7 - Graphics of Ohm's first law
- Graphic of an ohmic resistor
- Graph of a non-ohmic resistor
- 8 - Differences between Ohm's first law and Ohm's second law
- 9 - Solved exercises on Ohm's first law
Summary of Ohm's First Law
Ohm's first law states that if a potential difference is applied to a resistor at constant temperature, an electric current will flow through it.
It demonstrates the relationship between Electric tension, electrical resistance and electric current.
The electrical resistor is a piece of equipment that controls how much current will flow through the electrical circuit.
Electrical resistors can be ohmic or non-ohmic, both with resistance that can be calculated by the Ohm's laws.
All electrical resistors have the property of electrical resistance.
Using Ohm's first law formula, we find that resistance is equal to the division between voltage and electric current.
For an ohmic resistor, the graph of Ohm's first law is a straight line.
For a non-ohmic resistor, the graph of Ohm's first law is a curve.
The first and second Ohm's laws provide the calculation of electrical resistance, but relating it to different quantities.
Video on Ohm's First Law
What does Ohm's first law say?
Ohm's first law tells us that when we apply to the two terminals of a electrical resistor, à temperature constant, a potential difference (electrical voltage), it will be traversed by an electric current, as we can see below:

In addition, through its formula, we realize that the electrical resistance is proportional to the electrical voltage (ddp or electrical potential difference), but inversely proportional to the electrical current. So if we increase the voltage, the resistance will also increase. However, if we increase the current, the resistance will decrease.
\(R\propto U\ \)
\(R\propto\frac{1}{i}\)
Do not stop now... There's more after the ad ;)
What are resistors?
resistors are electrical devices with the function of controlling the passage of electric current in an electrical circuit, converting the electrical energy from the electrical voltage into Thermal energy or heat, which is known as joule effect.

If a resistor respects Ohm's first law, we call it a resistor. ohmic resistor, but if it does not respect Ohm's first law, it receives the nomenclature of non-ohmic resistor, regardless of what type it is. Both resistors are calculated by Ohm's law formulas. Most devices have non-ohmic resistors in their circuit, as is the case with calculators and cell phones.
What is electrical resistance?
Electrical resistance is the physical property that electrical resistors have to contain the transfer of electrical current to the rest of the electrical circuit. It is symbolized by a square or zigzag in the circuits:

Read too: Short circuit — when the electrical current does not encounter any kind of resistance in the electrical circuit
Ohm's first law formula
The formula corresponding to Ohm's first law is:
\(R=\frac{U}{i}\)
It can be rewritten as:
\(U=R\cdot i\)
u → potential difference (ddp), measured in Volts [V].
R → electrical resistance, measured in Ohm [Ω].
i → electric current, measured in Ampere [A].
Example:
A 100 Ω resistor has an electrical current of \(20\ mA\) crossing it. Determine the potential difference across the terminals of this resistor.
Resolution:
We will use Ohm's first law formula to find the ddp:
\(U=R\cdot i\)
\(U=100\cdot20\ m\)
O m in \(20\ mA\) means micro, which is worth \({10}^{-3}\), then:
\(U=100\cdot20\cdot{10}^{-3}\)
\(U=2000\cdot{10}^{-3}\)
transforming into cientific notation, we have:
\(U=2\cdot{10}^3\cdot{10}^{-3}\)
\(U=2\cdot{10}^{3-3}\)
\(U=2\cdot{10}^0\)
\(U=2\cdot1\)
\(U=2\V\)
The ddp between the resistor terminals is 2 Volts.
Ohm's first law graphs
The graph of Ohm's first law depends on whether we are working with an ohmic resistor or a non-ohmic resistor.
Graphic of an ohmic resistor
The graph for an ohmic resistor, one that obeys Ohm's first law, behaves like a straight line, as we can see below:
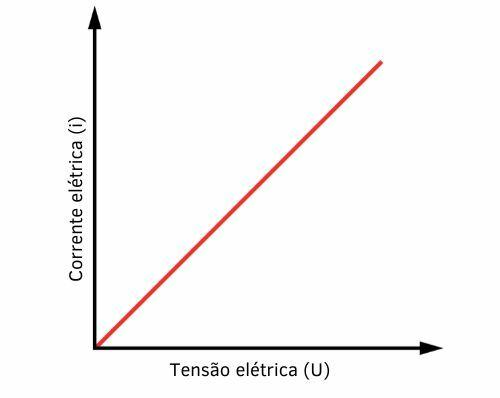
When working with graphs, we can calculate electrical resistance in two ways. The first is by substituting the current and voltage data into Ohm's first law formula. The second is through the tangent of the angle θ, by the formula:
\(R=tan{\theta}\)
R → electrical resistance, measured in Ohm [Ω].
θ → angle of inclination of the line, measured in degrees [°].
Example:
Using the graph, find the value of electrical resistance.
Resolution:
As we were not given information on the values of electric current and voltage, we will find the resistance through the tangent of the angle:
\(R=\tan{\theta}\)
\(R=tan45°\)
\(R=1\mathrm{\Omega}\)
So the electrical resistance is 1 Ohm.
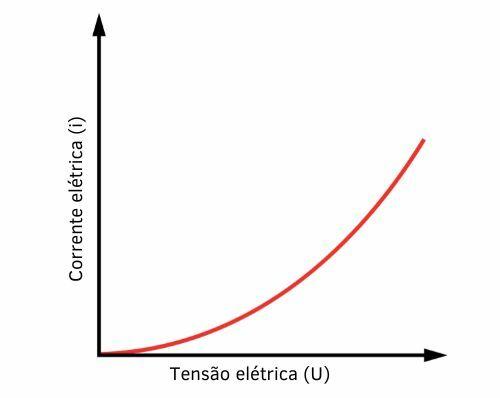
Graph of a non-ohmic resistor
The graph for a non-ohmic resistor, the one that does not obey Ohm's first law, behaves like a curve, as we can see in the graph below:
Differences between Ohm's First Law and Ohm's Second Law
Although the first and second Ohm's laws bring the formula for electrical resistance, they have differences in relation to the quantities we relate to electrical resistance.
Ohm's First Law: brings the relationship of electrical resistance with electrical voltage and electrical current.
Ohm's second law: informs that the electrical resistance varies according to the electrical resistivity and conductor dimensions. The greater the electrical resistivity, the greater the resistance.
Also know: 10 Essential Physics Equations for Enem
Solved exercises on Ohm's first law
question 1
(Vunesp) The nominal values of an incandescent lamp, used in a flashlight, are: 6.0 V; 20 mA. This means that the electrical resistance of your filament is:
A) 150 Ω, always, with the lamp on or off.
B) 300 Ω, always, with the lamp on or off.
C) 300 Ω with the lamp on and has a much higher value when off.
D) 300 Ω with the lamp on and has a much lower value when off.
E) 600 Ω with the lamp on and has a much higher value when off.
Resolution:
Alternative D
Using Ohm's first law:
\(U=R\cdot i\)
\(6=R\cdot20\ m\)
O m in \(20\ mA\) means micro, which is worth \({10}^{-3}\), then:
\(6=R\cdot20\cdot{10}^{-3}\)
\(R=\frac{6}{20\cdot{10}^{-3}}\)
\(R=\frac{0.3}{{10}^{-3}}\)
\(R=0.3\cdot{10}^3\)
\(R=3\cdot{10}^{-1}\cdot{10}^3\)
\(R=3\cdot{10}^{-1+3}\)
\(R=3\cdot{10}^2\)
\(R=300\ \mathrm{\Omega}\)
Resistance varies with temperature, so as the temperature of the filament is lower when the bulb is off, the resistance will also be lower.
question 2
(Uneb-BA) An ohmic resistor, when subjected to a ddp of 40 V, is crossed by an electric current of intensity 20 A. When the current flowing through it is equal to 4 A, the ddp, in volts, at its terminals will be:
a) 8
B) 12
C) 16
D) 20
E) 30
Resolution:
Alternative A
We will calculate the value of the resistor when it is passed through a current of 20 A and subjected to ddp of 40 V, using the formula of Ohm's first law:
\(U=R\cdot i\)
\(40=R\cdot20\)
\(\frac{40}{\ 20}=R\)
\(2\mathrm{\Omega}=R\)
We will use the same formula to find the ddp across the terminals when the resistor is passed through a current of 4 A.
\(U=R\cdot i\)
\(U=2\cdot4\)
\(U=8\V\)
By Pâmella Raphaella Melo
Physics teacher


