Mathematics Enem Simulation

Study for the Enem with our math simulation. There are 45 solved and commented questions on Mathematics and its Technologies, selected according to the most demanded subjects in the National High School Exam.

Pay attention to the simulation rules

• 4545 questions
• Maximum duration of 3 hours
• Your result and the template will be available at the end of the simulation

Simulated startedFinished simulationstart simulation

question 1

A builder needs to tile the floor of a rectangular room. For this task, he has two types of ceramics:

a) ceramic in the shape of a square with a side of 20 cm, which costs R$ 8.00 per unit;

b) ceramic in the shape of an isosceles right triangle with 20 cm legs, which costs R$ 6.00 per unit.

The room is 5 m wide and 6 m long.

The builder wants to spend the least amount possible on the purchase of ceramics. Let x be the number of square-shaped ceramic pieces and y be the number of triangular-shaped ceramic pieces.

This then means finding values ​​for x and y such that 0.04x + 0.02y > 30 and that make the smallest possible value of

The) 8x + 6y.

B) 6x + 8y.

ç) 0.32x + 0.12y.

d) 0.32x + 0.02y.

and) 0.04x + 0.12y.

feedback explained

The expression of the price depends on the quantity x of square coverings of R$8.00 plus y triangular coverings of R$6.00.

8. x + 6. and

8x + 6y

question 2

A blood group, or blood type, is based on the presence or absence of two antigens, A and B, on the surface of red blood cells. As two antigens are involved, the four distinct blood types are:

• Type A: only antigen A is present;

• Type B: only the B antigen is present;

• Type AB: both antigens are present;

• Type O: none of the antigens are present.

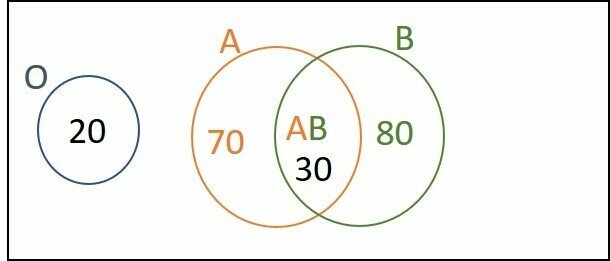
Blood samples were collected from 200 people and, after laboratory analysis, it was identified that in 100 samples antigen A is present, in 110 samples there is presence of antigen B and in 20 samples none of the antigens is present. gift. Of those people who have had blood drawn, the number of those who have blood type A is equal to 

The) a) 30.

B) b) 60.

ç) c) 70

d) d) 90.

and) e) 100.

feedback explained

This is a question about sets.

Consider the universe set with 200 elements.

Of these 20 are type O. So 200 - 20 = 180 can be A, B or AB.

There are 100 A antigen carriers and 110 B antigen carriers. Since 100 + 110 = 210, there must be an intersection, people with AB blood.

This intersection must have, 210 - 180 = 30 individuals, of type AB.

Of the 100 A antigen carriers, there remain 100 - 30 = 70 people with A antigen alone.

Conclusion
Therefore, 70 people have type A blood.

question 3

One company specializes in leasing containers that are used as mobile commercial units. The standard model rented by the company has a height of 2.4 m and the other two dimensions (width and length), 3.0 m and 7.0 m, respectively.

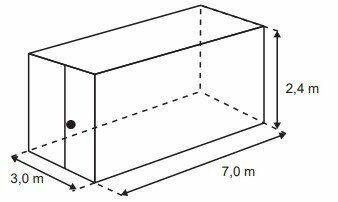
A customer requested a container with a standard height, but with a width 40% greater and a length 20% less than the corresponding measurements of the standard model. To meet market needs, the company also has a stock of other container models, as shown in the table.

Of the available models, which one meets the customer's needs?

The) I

B) II

ç) III

d) IV

and) V

feedback explained

40% wider width.

To increase 40% just multiply by 1.40.

1.40 x 3.0 = 4.2 m 

20% shorter length

To decrease 20% just multiply by 0.80.

0.80 x 7.0 = 5.6 m

Conclusion

Model II meets customer needs.

4.2 m wide and 5.6 m long.

question 4

Two athletes start from points, respectively P1 and P2, on two different flat tracks, as shown in the figure, moving counterclockwise to the finish line, thus covering the same distance (L). The straight sections from the ends of the turns to the finish line of this course have the same length (l) on both lanes and are tangent to the curved sections, which are semicircles with center C. The radius of the major semicircle is R1 and the radius of the minor semicircle is R2 .

It is known that the length of a circular arc is given by the product of its radius and the angle, measured in radian, subtended by the arc. Under the conditions presented, the ratio of the angle measure  by the difference L−l is given by

The) R2− R1

B) 1/R1 - 1/R2

ç) 1/R2 - 1/R1

d) 1/R2 - R1

and) 1/R1 + 1/R2

feedback explained

objective
determine the reason 

Data
L is the total length and is the same for both athletes.
l is the length of the straight part and is the same for both athletes.

Step 1: Determine 

Calling the angle of athlete 1 and the angle of athlete 2, the angle  is the difference between the two.

As stated in the statement, the arc is the product of the radius and the angle.

Substituting into the previous equation:

Step 2: Determine L - l

Calling d1 the curved distance covered by athlete 1, he covers in total:

L = d1 + l

Calling d2 the curved distance covered by athlete 2, he covers in total:

L = d2 + l

This implies that d1 = d2, since as l and L are the same for both athletes, the curved distances must also be equal. Soon

d1 = L - l
d2 = L - l

And, d1 = d2

Step 3: Determine the reason 

Replacing d1 with d2,

Conclusion

The answer is 1/R2 - 1/R1.

question 5

A decorative vase broke and the owners will order another one to be painted with the same characteristics. They send a 1:5 scale photo of the vase (relative to the original object) to an artist. To better see the details of the vase, the artist requests a printed copy of the photo with dimensions tripled in relation to the dimensions of the original photo. In the printed copy, the broken vase has a height of 30 centimeters.

What is the actual height, in centimeters, of the broken vase?

The) 2

B) 18

ç) 50

d) 60

and) 90

feedback explained

objective
Determine the actual height of the vase.

Calling the original height h

First moment: photo

The photo uploaded is in 1:5 scale, which is to say it is five times smaller than the vase.
In this photo, the height is 1/5 of the actual height.

Second moment: enlarged hard copy

The hard copy is tripled in dimensions (3:1), which means it is 3 times larger than the photo.
In the copy, the height is 3 times greater than in the photo and is 30 cm.

Conclusion
The original vase is 50 cm high.

question 6

After the end of registration for a contest, whose number of vacancies is fixed, it was announced that the ratio between the number of candidates and the number of vacancies, in that order, was equal to 300. However, enrollment was extended, with 4,000 more candidates signing up, bringing the aforementioned ratio to 400. All registered candidates took the test, and the total number of successful candidates was equal to the number of vacancies. The other candidates were rejected.

Under these conditions, how many candidates failed?

The) 11 960

B) 11 970

ç) 15 960 

d) 15 970

and) 19 960

feedback explained

objective
Determine the number of failures.

Step 1: number of disapproved.

R = TC - V

Being,
R the number of failures;
TC the total number of candidates;
V the number of vacancies (approved).

The total number of TC candidates is the initial number of registered C candidates plus 4000.

TC = C + 4000

Thus, the number of failures is:

Step 2: First time of registration.

So, C = 300V

Step 3: second moment of registration.

Substituting the value of C and isolating V.

Substituting V = 40 into C = 300V.

C = 300. 40 = 12 000

We have,
V = 40 (total vacancies or approved candidates) 
C = 12 000 

Substituting into the equation from step 1:

Conclusion
15,960 candidates failed the contest.

question 7

In the isosceles trapezoid shown in the following figure, M is the midpoint of the segment BC, and the points P and Q are obtained by dividing the segment AD into three equal parts.

Line segments are drawn through points B, M, C, P and Q, determining five triangles inside the trapezoid, as shown in the figure. The ratio of BC to AD that determines equal areas for the five triangles shown in the figure is

The) 1/3

B) 2/3 

ç) 2/5

d) 3/5

and) 5/6

feedback explained

The five triangles have the same area and the same height, because the distance between the bases of the trapezoid are equal at any point, since BC and AD are parallel.

Since the area of ​​a triangle is determined by  and all have the same area, this implies that the bases are also equal to all.

So BC = 2b and Ad = 3b

So the reason is:

question 8

A Brazilian theme park built a miniature replica of Liechtenstein's castle. The original castle, represented in the image, is located in Germany and was rebuilt between the years 1840 and 1842, after two destructions caused by wars.

The castle has a bridge that is 38.4 m long and 1.68 m wide. The craftsman who worked for the park produced a replica of the castle, to scale. In this work, the measurements of the length and width of the bridge were, respectively, 160 cm and 7 cm.

The scale used to make the replica is

The) 1: 576

B) 1: 240

ç) 1: 24 

d) 1: 4,2

and) 1: 2,4

feedback explained

The scale is O: R

Where O is the original measurement and R is the replica.

Taking the length measurement:

So the scale is 1:24.

question 9

A map is a reduced and simplified representation of a location. This reduction, which is done using a scale, maintains the proportion of the represented space in relation to the real space.

A certain map has a scale of 1: 58 000 000.

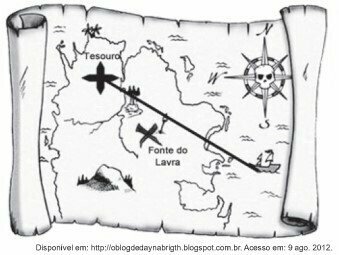
Assume that, on this map, the line segment connecting the ship to the treasure mark measures 7.6 cm.

The actual measurement, in kilometers, of this line segment is

The) 4 408.

B) 7 632.

ç) 44 080.

d) 76 316.

and) 440 800.

feedback explained

The scale of the map is 1: 58 000 000 

This means that 1 cm on the map is equivalent to 58 000 000 cm on the real terrain.

Converting to kilometer, we divide by 100 000.

58 000 000 / 100 000 = 580 km.

Setting up the proportion:

question 10

The table shows the list of players who were part of the Brazilian men's volleyball team at the 2012 Olympics, in London, and their respective heights, in meters.

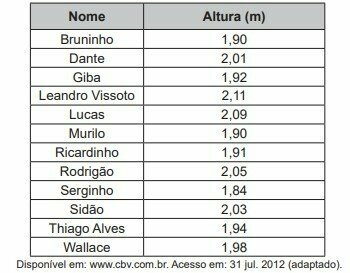
The median height, in meters, of these players is

The) 1,90.

B) 1,91.

ç) 1,96.

d) 1,97.

and) 1,98.

feedback explained

The median is a measure of central tendency and it is necessary to organize the data in an ascending way.

As the amount of data is even (12), the median is the arithmetic mean of the central measures.

question 11

An airline launches a weekend promotion for a commercial flight. For this reason, the customer cannot make reservations and the seats will be randomly drawn. The figure shows the position of the seats on the plane:

Because he is terrified of sitting between two people, a passenger decides that he will only travel if the chance of taking one of these seats is less than 30%.

Evaluating the figure, the passenger gives up the trip, because the chance of him being drawn with an armchair between two people is closer to

The) 31%.

B) 33%.

ç) 35%.

d) 68%.

and) 69%.

feedback explained

Probability is a ratio between the number of favorable cases and the total number.

Total seats

The total number of seats on the plane is:

38 x 6 - 8 = 220 seats.

Notice that there are 8 spaces without seats.

uncomfortable armchairs

38 x 2 (those between two) minus 8, which have empty spaces near windows.

38 x 2 - 8 = 68

The probability is:

in percentage

0.3090 x 100 = 30.9%

Conclusion
The probability of the passenger being seated between two people is approximately 31%.

question 12

The Human Development Index (HDI) measures the quality of life of countries beyond economic indicators. The HDI in Brazil has grown year after year and reached the following levels: 0.600 in 1990; 0.665 in 2000; 0.715 in 2010. The closer to 1.00, the greater the development of the country.

The globe. Economics Notebook, 3 Nov. 2011 (adapted).

Observing the behavior of the HDI in the aforementioned periods, it can be seen that, over the period 1990-2010, the Brazilian HDI

The) decreased with increasing decennial variations.

B) decreased in direct proportion to time.

ç) increased with decreasing decennial variations.

d) increased in direct proportion to time.

and) increased in inverse proportion with time.

feedback explained

The variation between 2000 and 1990 was:

HDI 2000 - HDI 1990
0,665 - 0,600 = 0,065

The variation between 2010 and 2000 was:

HDI 2010 - HDI 2000
0,715 - 0,665 = 0,050

Thus, the HDI increased with decreasing decennial variations.

question 13

A loan agreement provides that when an installment is paid in advance, an interest reduction will be granted according to the period of anticipation. In this case, the present value is paid, which is the value, at that moment, of an amount that should be paid at a future date. A present value P subjected to compound interest at rate i, for a period of time n, produces a future value V determined by the formula

In a loan agreement with sixty fixed monthly installments, of R$ 820.00, at an interest rate of 1.32% per month, together with with the thirtieth installment, another installment will be paid in advance, provided that the discount is greater than 25% of the value of the portion.

Use 0.2877 as an approximation to  and 0.0131 as an approximation to In (1.0132).

The first of the installments that can be brought forward together with the 30th is the

The) 56ª

B) 55ª

ç) 52ª 

d) 51ª

and) 45ª

feedback explained

objective 
Calculate the number of the installment that must be brought forward to produce a 25% discount on the present value.

The parcel number is 30+n. Where 30 is the number of the current installment and n is the number of installments ahead required.

V is the value of the installment, R$820.00.
P is the value of the advance installment.
i is the rate 1.32% = 0.0132
n is the number of parcels 

The amount to be paid in the advance installment must be at least 25% lower than the amount of R$820.00.

From the compound interest formula given by the question, we have:

Applying the logarithm on both sides of the equality:

By the property of logarithms, the exponent n starts to multiply the logarithm.

Substituting the values ​​given in the question:

So adding 22 + 30 = 52.

Conclusion
The advance installment must be the 52nd.

question 14

Camile likes to walk on a sidewalk around a circular square that is 500 meters long, located close to her house. The square, as well as some places around it and the point from where the walk starts, are represented in the figure:

One afternoon, Camile walked 4,125 meters, counterclockwise, and stopped.

Which of the locations indicated in the figure is closest to your stop?

The) Cultural Center.

B) Drugstore.

ç) LAN house.

d) Starting point.

and) The bakery.

feedback explained

The statement says that one lap is 500 m. Care must be taken not to confuse length with diameter.

After 8 complete turns it stops at the starting point again, and advances another 1/4 turn counterclockwise, arriving at the bakery.

question 15

The mayor of a city wants to promote a popular party in the municipal park to commemorate the founding anniversary of the municipality. It is known that this park has a rectangular shape, 120 m long by 150 m wide. In addition, for the safety of those present, the police recommend that the average density, in an event of this nature, does not exceed four people per square meter.

Following the safety recommendations established by the police, what is the maximum number of people that can be present at the party?

The) 1 000

B) 4 500

ç) 18 000

d) 72 000

and) 120 000

feedback explained

The area of ​​the square is 120 x 150 = 18,000 m².

With 4 people per square meter, we have:

18,000 x 4 = 72,000 people.

question 16

A zootechnician wants to test whether a new feed for rabbits is more efficient than the one he is currently using. The current feed provides an average mass of 10 kg per rabbit, with a standard deviation of 1 kg, fed this feed over a period of three months.

The zootechnician selected a sample of rabbits and fed them the new feed for the same period of time. At the end, he recorded the mass of each rabbit, obtaining a standard deviation of 1.5 kg for the distribution of the masses of the rabbits in this sample.

To evaluate the efficiency of this ration, he will use the coefficient of variation (CV) which is a measure of dispersion defined by CV = , where s represents the standard deviation and , the average of the masses of rabbits that were fed a given ration.

The zootechnician will replace the feed he was using with the new one, if the coefficient of variation of the distribution of the masses of the rabbits that were fed the new chow is smaller than the coefficient of variation of the mass distribution of the rabbits that were fed the chow current.

Feed replacement will occur if the mean of the distribution of the masses of the rabbits in the sample, in kilograms, is greater than

The) 5,0.

B) 9,5.

ç) 10,0.

d) 10,5.

and) 15,0.

feedback explained

For substitution to occur, the condition is:

New CV < Current CV

Data with the current ration.

current CV = 

Data with the new ration.

To determine the x needed for substitution to occur:

question 17

The number of fruits of a given plant species is distributed according to the probabilities shown in the table.

The probability that, on such a plant, there are at least two fruits is equal to

The) 3%.

B) 7%.

ç) 13%.

d) 16%.

and) 20%.

feedback explained

At least two implies there are two or more.

P(2) or P(3) or P(4) or P(5) = 0.13 + 0.03 +0.03 + 0.01 = 0.20 or 20%

question 18

The urbanization rate of a municipality is given by the ratio between the urban population and the total population of the municipality (that is, the sum of the rural and urban populations). The graphs show, respectively, the urban population and the rural population of five municipalities (I, II, III, IV, V) in the same state region. In a meeting between the state government and the mayors of these municipalities, it was agreed that the municipality with the highest urbanization rate will receive an extra investment in infrastructure.

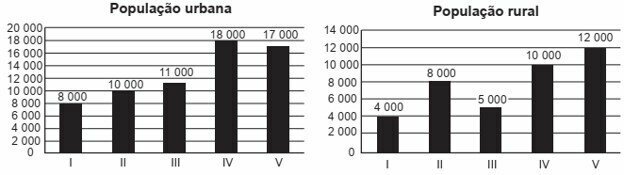
According to the agreement, which municipality will receive the extra investment?

The) I

B) II

ç) III

d) IV

and) V

feedback explained

The urbanization rate is given by:

Checking for each municipality:

Municipality I

Municipality II

Municipality III

Municipality IV

Municipality V

Therefore, the highest urbanization rate is that of municipality III.

question 19

Isaac Newton's Law of Gravitation establishes the magnitude of the force between two objects. It is given by the equation , where m1 and m2 are the masses of the objects, d the distance between them, g the universal constant of gravitation and F the intensity of the gravitational force that one object exerts on the other.

Consider a scheme that represents five satellites of the same mass orbiting the Earth. Denote the satellites by A, B, C, D and E, this being the decreasing order of distance from Earth (A the farthest and E the closest to Earth).

According to the Law of Universal Gravitation, the Earth exerts the greatest force on the satellite

The) THE.

B) B.

ç) Ç.

d) D.

and) AND.

feedback explained

As in the formula d is in the denominator and the larger its value, the smaller the force, as it will be a division by a larger number. Thus, the gravitational force decreases with increasing distance.

So for a smaller d, the force is larger.

Therefore, satellite E and Earth form the greatest gravitational force.

question 20

A tube factory packs smaller cylindrical tubes inside other cylindrical tubes. The figure shows a situation where four cylindrical tubes are packed neatly into a tube with a larger radius.

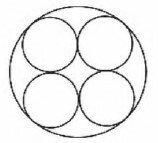
Suppose you are the operator of the machine that will produce the larger tubes in which four inner cylindrical tubes will be placed, without adjustments or clearances.

If the base radius of each of the smaller cylinders is equal to 6 cm, the machine you operate must be adjusted to produce larger tubes with a base radius equal to

The) 12 cm.

B) 12 √2cm .

ç) 24 √2 cm .

d) 6(1+√2) cm.

and) 12(1+√2) cm.

feedback explained

By joining the radii of the smaller circles we form a square:

The radius of the larger circle is half the diagonal of this square plus the radius of a smaller circle.

Where,
R is the radius of the larger circle.
d is the diagonal of the square.
r is the radius of the smaller circle.

To determine the diagonal of the square, we use the Pythagorean theorem, where the diagonal is the hypotenuse of the triangle with sides equal to r + r = 12.

Substituting the value of d into the equation of R, we have:

Equating the denominators,

Factoring 288, we have:

288 = 2. 2². 2². 3²

The root of 288 becomes:

Substituting into the R equation:

Putting 12 in evidence and simplifying,

question 21

A person will produce a costume using as materials: 2 different types of fabrics and 5 different types of ornamental stones. This person has 6 different fabrics and 15 different ornamental stones at their disposal.

The amount of costumes with different materials that can be produced is represented by the expression

The)

B)

ç)

d)

and)

feedback explained

By the multiplicative principle we have that the number of possibilities is the product of:

fabric options x stone options

As 2 fabrics out of 6 will be chosen, we must know in how many ways we can choose 2 fabrics from a set of 6 different fabrics.

Regarding the stones, we will choose 5 stones from a set of 15 different ones, so:

Therefore, the amount of costumes with different materials that can be produced is represented by the expression:

question 22

The probability that an employee will remain in a particular company for 10 years or more is 1/6.

A man and a woman start working at this company on the same day. Assume that there is no relationship between his work and hers, so that their length of stay at the firm is independent of each other.

The probability that both a man and a woman will remain in this company for less than 10 years is

The) 60/36

B) 25/36

ç) 24/36

d) 12/36

and) 1/36

feedback explained

The probability of staying for more than 10 years is 1/6, so the probability of staying for less than 10 years is 5/6 for each employee.

Since we want the probability that the two leave before 10 years, we have:

question 23

A glazier is hired to place a sliding glass door in a channel with an internal width of 1.45 cm, as shown in the figure.

The glazier needs a glass plate as thick as possible, such that it leaves a total gap of at least 0.2 cm, so that the glass can slip in the channel, and a maximum of 0.5 cm so that the glass does not hit with the interference of the wind after the installation. To get this glass plate, this glazier went to a store and there he found glass plates with thicknesses equal to: 0.75 cm; 0.95 cm; 1.05 cm; 1.20 cm; 1.40 cm.

To meet the specified restrictions, the glazier must purchase the plate with a thickness, in centimeters, equal to

The) 0,75.

B) 0,95.

ç) 1,05.

d) 1,20.

and) 1,40.

feedback explained

minimum clearance

The channel thickness, 1.45 cm, minus the thickness of the glass, must allow a gap of at least 0.20 cm.

1.45 - 0.20 = 1.25 cm

maximum clearance

The channel thickness, 1.45 cm, minus the thickness of the glass must allow a gap of a maximum of 0.50 cm.

1.45 - 0.50 = 0.95 cm

Thus, the thickness of the glass should be between 0.95 and 1.25 cm, being as thick as possible.

Conclusion
Among the options, the 1.20 cm glass is in the range and is the largest available.

question 24

An athlete produces his own meal with a fixed cost of R$ 10.00. It consists of 400 g of chicken, 600 g of sweet potato and a vegetable. Currently, the prices of products for this meal are:

In relation to these prices, there will be a 50% increase in the price per kilogram of sweetpotato, and the other prices will not change. The athlete wants to keep the cost of the meal, the amount of sweet potato and the vegetable. Therefore, you will have to reduce the amount of chicken.

What percentage reduction must be in the amount of chicken for the athlete to reach his goal?

The) 12,5

B) 28,0

ç) 30,0 

d) 50,0 

and) 70,0

feedback explained

Data
Fixed cost
400 g of chicken at R$12.50 per kg.
600 g sweet potato at R$ 5.00 kg.
1 vegetable

50% increase in sweet potato price.

objective
Determine the percentage reduction of chicken in the meal that maintains the price after the increase.

current cost
Converting the mass from g to kg.

0.4 x 12.50 = R$ 5.00 of chicken.
0.6 x 5.00 = BRL 3.00 of sweet potato.
R$ 2.00 for the vegetable.

Increase in the price of sweet potato.
5.00 + 50% of 5.00
5.00 x 1.50 = BRL 7.50 

new cost
0.6 x 7.5 = BRL 4.50 of sweet potato
R$ 2.00 for the vegetable.

The subtotal is: 4.50 + 2.00 = 6.50.

Thus, there are 10.00 - 6.50 = 3.50 left to buy the chicken.

new amount of chicken
12.50 buys 1000g
3.50 buy xg

Making a rule of three:

percentage reduction

This means that there was a reduction of 0.30, since 1.00 - 0.70 = 0.30.

Conclusion
The athlete must reduce the amount of chicken by 30% to maintain the price of the meal.

question 25

A graphics technician builds a new sheet from the measurements of an A0 sheet. The measurements of an A0 sheet are 595 mm wide and 840 mm long.

The new sheet is constructed as follows: it adds an inch to the width measurement and 16 inches to the length measurement. This technician needs to know the ratio of the width and length measurements, respectively, of this new sheet.

Consider 2.5 cm as an approximate value for an inch.

What is the ratio of the width and length measurements of the new sheet?

The) 1/16

B) 620/1240

ç) 596/856 

d) 598/880

and) 845/4840

feedback explained

Converting measurements to millimeters:

Width = 595mm + (1. 2,5. 10) mm = 620 mm
Length = 840mm + (16. 2,5. 10) mm = 1 240 mm

The reason is:

620/1240 

question 26

In the construction of a housing complex of popular houses, all will be made in the same model, occupying, each of them, land whose dimensions are equal to 20 m in length by 8 m in width. Aiming at the commercialization of these houses, before the beginning of the works, the company decided to present them through models built in a scale of 1: 200.

The measurements of the length and width of the plots, respectively, in centimeters, in the model built, were

The) 4 and 10.

B) 5 and 2.

ç) 10 and 4.

d) 20 and 8.

and) 50 and 20.

feedback explained

Converting land measurements to centimeters:

20 m = 2000 cm

8 m = 800 cm

As the scale is 1:200 we must divide the terrain measurements by 200.

2000 / 200 = 10

800 / 20 = 4

Conclusion
The answer is: 10 and 4.

Question 27

For certain springs, the spring constant (C) depends on the average diameter of the spring circumference (D), the number of useful spirals (N), the diameter (d) of the metal wire from which the spring is formed and the modulus of elasticity of the material (G). The formula highlights these dependency relationships.

A factory owner has a spring M1 in one of his equipment, which has characteristics D1, d1, N1 and G1, with an elastic constant C1. This spring needs to be replaced by another, M2, produced with another material and with different characteristics, as well as a new spring constant C2, as follows: I) D2 = D1/3; II) d2 = 3d1; III) N2 = 9N1. Also, the elasticity constant G2 of the new material is equal to 4 G1.

The value of constant C2 as a function of constant C1 is

The) C2 = 972⋅C1

B) C2 = 108⋅C1

ç) C2 = 4⋅C1

d) C2 = 4/3. C1

and) C2 = 4/9. C1

feedback explained

The second spring is:

The values ​​of constants 2 are:

D2 = D1/3
d2 = 3d1
N2 = 9N1
G2 = 4G1

Substituting and doing the calculations:

Passing the coefficients forward:

We can substitute for C1 and calculate the new coefficient.

question 28

The international standard ISO 216 defines the paper sizes used in almost all countries. The base format is a rectangular sheet of paper called A0, whose dimensions are in the ratio 1 :√2. From then on, the sheet is folded in half, always on the longest side, defining the other formats, according to the folding number. For example, A1 is sheet A0 folded in half once, A2 is sheet A0 folded in half twice, and so on, as shown.

A very common paper size in Brazilian offices is A4, whose dimensions are 21.0 cm by 29.7 cm.

What are the dimensions, in centimeters, of the A0 sheet?

The) 21.0 x 118.8

B) 84.0 x 29.7

ç) 84.0 x 118.8

d) 168.0 x 237.6

and) 336.0 x 475.2

feedback explained

The dimensions of the A0 sheet are four times the dimensions of the A4 sheet. Soon:

question 29

A country decides to invest resources in education in its cities that have a high level of illiteracy. The resources will be divided according to the average age of the population that is illiterate, as shown in the table.

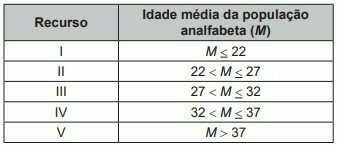
A city in that country has 60/100 of the illiterate population of its population composed of women. The average age of illiterate women is 30 years, and the average age of illiterate men is 35 years.

Considering the average age of the illiterate population of this city, it will receive the 

The) I.

B) II.

ç) III.

d) IV.

and) v.

feedback explained

This is a weighted average.

According to the options, the answer is option c.

Appeal III 

question 30

Students taking a math course at a university want to make a graduation plaque, in the form of a equilateral triangle, in which their names will appear within a square region, inscribed on the plate, according to the figure.

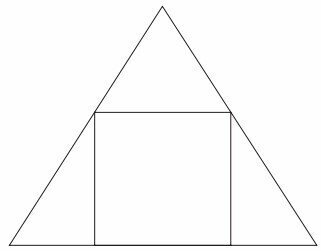
Considering that the area of ​​the square, in which the names of the trainees will appear, measures 1 m², what is the approximate measurement, in meters, of each side of the triangle that represents the plate? (Use 1.7 as an approximate value for √3 ).

The) 1,6

B) 2,1

ç) 2,4

d) 3,7

and) 6,4

feedback explained

Since the triangle is equilateral, the three sides are equal and the interior angles are equal to 60º.
Since the area of ​​the square is 1 m², its sides measure 1 m.

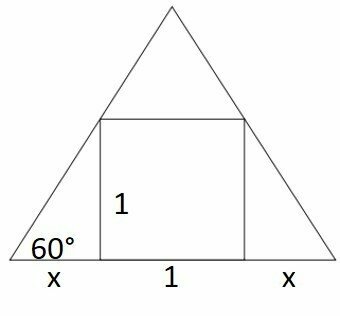
The base of the triangle is x + 1 + x, so:

L = 2x + 1

Where L is the length of the side of the triangle.

The 60 degree tangent is:

As the statement gives the approximate value of the root of 3, let's substitute in the formula L = 2x + 1.

Question 31

A construction company intends to connect a central reservoir (Rc) in the shape of a cylinder, with an internal radius equal to 2 m and an internal height equal to 3.30 m, to four auxiliary cylindrical reservoirs (R1, R2, R3 and R4), which have internal radii and internal heights measuring 1.5 m.

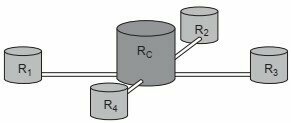
The connections between the central reservoir and the auxiliary ones are made by cylindrical pipes with 0.10 m of internal diameter and 20 m of length, connected close to the bases of each reservoir. In the connection of each of these pipes with the central reservoir there are registers that release or interrupt the flow of water.

When the central reservoir is full and the auxiliaries are empty, the four valves are opened and, after a while, the heights of the water columns in the reservoirs are equal, as soon as the flow of water between them ceases, by the principle of the vessels communicators.

The measurement, in meters, of the heights of the water columns in the auxiliary reservoirs, after the flow of water between them has ceased, is

The) 1,44.

B) 1,16.

ç) 1,10.

d) 1,00.

and) 0,95.

feedback explained

The height of the water column will be the same, including the central reservoir.

Initial volume in RC.

A part of this volume will flow into the smaller tubes and reservoirs, but the volume in the system remains the same before and after the flow.

Volume in Rc = 4. volume in the pipes + 4. reservoir volume + volume left in Rc

The desired height is h.

Putting  in evidence, simplifying and solving for h, we have:

question 32

In a study carried out by the IBGE in four states and the Federal District, with more than 5 thousand people with 10 years or more, it was observed that reading occupies, on average, only six minutes of each day. person. In the age group of 10 to 24 years, the daily average is three minutes. However, in the age group between 24 and 60 years old, the average daily time devoted to reading is 5 minutes. Among the oldest, aged 60 and over, the average is 12 minutes.

The number of people interviewed in each age group followed the percentage distribution described in the table.

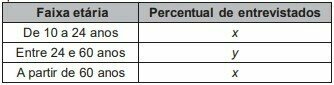
Available at: www.oglobo.globo.com. Accessed on: 16 Aug. 2013 (adapted).

The x and y values ​​of the frame are, respectively, equal to

The) 10 and 80.

B) 10 and 90.

ç) 20 and 60.

d) 20 and 80.

and) 25 and 50.

feedback explained

The total percentage of respondents is:

x + y + x = 100%

2x + y = 1 (equation I)

The overall average reading is 6 min. This average is weighted by the quantities x and y.

Substituting into Equation I

Substituting the value of x in equation I

In percentage terms,

x = 1/5 = 0.20 = 20%

y = 3/5 = 0.60 = 60%

Question 33

In March 2011, an earthquake measuring 9.0 magnitude on the Richter scale hit Japan killing thousands of people and causing great destruction. In January of that year, an earthquake measuring 7.0 on the Richter scale hit the city of Santiago Del Estero, Argentina. The magnitude of an earthquake, measured on the Richter scale, is , where A is the amplitude of vertical ground motion, reported on a seismograph, A0 is a reference amplitude, and log represents the logarithm to base 10.

Available in: http://earthquake.usgs.gov. Accessed on: 28 Feb. 2012 (adapted).

The ratio between the amplitudes of the vertical motions of the earthquakes in Japan and Argentina is

The) 1,28

B) 2,0

ç)

d) 100

and)

feedback explained

The objective is to determine 

Being the magnitude of the Japan earthquake and  the magnitude of the earthquake in Argentina.

From the definition of logarithm 

We can write 

Using the definition of logarithm in the relationship provided in the statement:

With,

b=10 (base 10 does not need to be written)
c = R
a = A/A0

For the Japan earthquake:

For the Argentine quake:

Matching the reference values 

Question 34

Due to the failure to meet the targets set for the vaccination campaign against the common flu and the H1N1 virus in one year, the Ministry of Health announced the extension of the campaign for another week. The table shows the numbers of people vaccinated among the five risk groups up to the start date of the extension of the campaign.

What percentage of the total people in these risk groups are already vaccinated?

The) 12

B) 18

ç) 30

d) 40

and) 50

feedback explained

The total population at risk is: 4.5 + 2.0 + 2.5 + 0.5 + 20.5 = 30

The total already vaccinated is: 0.9 + 1.0 + 1.5 + 0.4 + 8.2 = 12

Question 35

A cyclist wants to assemble a gearing system using two toothed discs on the back of his bicycle, called ratchets. The crown is the toothed disc that is moved by the bicycle pedals, and the chain transmits this movement to the ratchets, which are positioned on the rear wheel of the bicycle. The different gears are defined by the different diameters of the ratchets, which are measured as indicated in the figure.

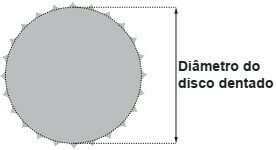
The cyclist already has a ratchet with a diameter of 7 cm and intends to include a second ratchet, so that, as the chain pass through it, the bike advances 50% more than it would if the chain passed through the first ratchet, each complete turn of the pedals.

The value closest to the measurement of the diameter of the second ratchet, in centimeters and to one decimal place, is

The) 2,3.

B) 3,5.

ç) 4,7.

d) 5,3.

and) 10,5.

feedback explained

The circumference of the circle is given by:

The radius of the first ratchet is 3.5 cm.

For the first ratchet we have:  for a turn.

For the second, there should be a 50% increase in forward, or another half turn.

If a full turn are , half turn is . So, one and a half turns are .

With the same turn of  now we want the bike to move forward .

Since the diameter is twice the radius:

The closest alternative is letter c) 4,7.

Question 36

In developing a new drug, researchers monitor the amount Q of a substance circulating in a patient's bloodstream, over time t. These researchers control the process by noting that Q is a quadratic function of t. The data collected in the first two hours were:

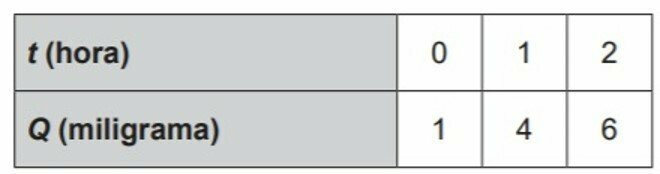
To decide whether to interrupt the process, avoiding risks to the patient, researchers want to know, in advance, the amount of the substance that will be circulating in this patient's bloodstream one hour after the last data collected.

Under the above conditions, this amount (in milligrams) will be equal to

The) 4.

B) 7.

ç) 8.

d) 9.

and) 0.

feedback explained

objective
Determine the quantity Q at the instant t=3.

The role is 2nd grade

To determine the coefficients a, b and c, we substitute the values ​​from the table, for each instant t.

For t = 0, Q = 1

For t = 1, Q = 4

For t = 2, Q = 6

Isolating a in equation I

3 = a + b
a = 3 - b

Substituting into Equation II

5 = 4(3-b) + 2b
5 = 12 - 4b + 2b
5 = 12 -2b
2b = 12 - 5
2b = 7
b = 7/2

Once b has been determined, we again substitute its value.

a = 3 - b
a = 3 - 7/2
a = -1/2

Substituting the values ​​of a, b and c into the general formula and calculating for t = 3.

a = -1/2
b = 7/2
c = 1

Question 37

The percussion instrument known as a triangle is composed of a thin steel bar, bent in a shape that resembles a triangle, with an opening and a stem, as shown in Figure 1.

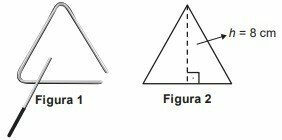
A promotional gifts company hires a foundry to produce miniature instruments of this type. The foundry initially produces pieces in the shape of an equilateral triangle of height h, as shown in Figure 2. After this process, each piece is heated, deforming the corners, and cut at one of the vertices, giving rise to the thumbnail. Assume that there are no material losses in the production process, so that the length of the bar used is equal to the perimeter of the equilateral triangle shown in Figure 2.

Consider 1.7 as an approximate value for √3.

Under these conditions, the value that most closely approximates the measurement of the length of the bar, in centimeters, is

The) 9,07.

B) 13,60.

ç) 20,40.

d) 27,18.

and) 36,24.

feedback explained

objective
Determine the length of the bar, which is the perimeter of the triangle.

Resolution
The perimeter of the triangle is 3L, since L + L + L = 3L.

From figure 2, considering half of the original equilateral triangle, we have a right triangle.

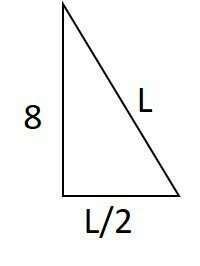
Using the Pythagorean theorem:

Rationalizing to remove the root of the denominator:

Since the perimeter is equal to 3L

question 38

Due to strong winds, an oil exploration company decided to reinforce the security of its offshore platforms, placing steel cables to better affix the central tower.

Assume that the cables will be perfectly stretched and will have one end at the midpoint of the lateral edges of the central tower (regular quadrangular pyramid) and the other at vertex of the platform base (which is a square with sides parallel to the sides of the base of the central tower and center coincident with the center of the base of the pyramid), as suggested by the illustration.

If the height and edge of the base of the central tower measure 24 m and 6√2 m, respectively, and the base side of the platform measures 19√2 m, then the measurement, in meters, of each cable will be equal to

The) √288

B) √313

ç) √328

d) √400

and) √505

feedback explained

objective
Determine the length of each cable.

Data
The cable is fixed at the midpoint of the edge of the pyramid.
Tower height 24 m.
Measure from the edge of the base of the pyramid 6√2 m.
Edge measurement on the platform side 19√2 m.

Resolution
To determine the length of the cable, we determined the height of the attachment point in relation to the base of the pyramid and the distance from the projection of the cable, to the attachment at the apex of the platform.

Once we have both measurements, a right triangle is formed and the length of the cable is determined by the Pythagorean theorem.

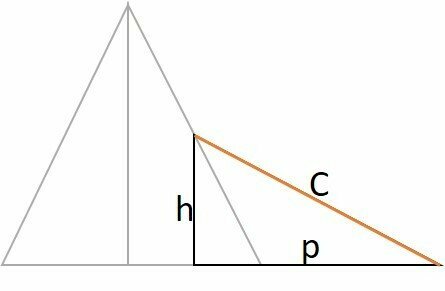
C is the length of the cable (purpose of the question)
h height from the base of the platform.
p is the projection of the cable at the base of the platform.

Step 1: height of the attachment point in relation to the platform base.
Analyzing the pyramid in its side view, we can determine the height at which the cable is fixed in relation to the base of the platform.

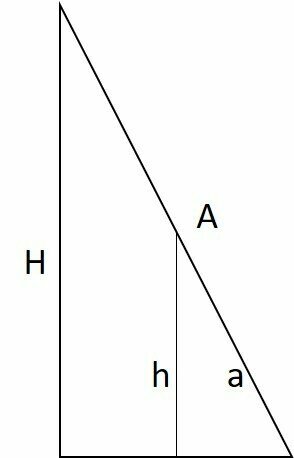
The smaller triangle is similar to the larger one, since its angles are equal.

The proportion:

Where,
H is the height of the pyramid = 24 m.
h is the height of the smaller triangle.
The edge of the tower.
a is the hypotenuse of the smaller triangle.

Since the cable is at the midpoint of A, the hypotenuse of the smaller triangle is half of A.

Substituting in proportion, we have:

So h = 24/2 = 12 m

Step 2: projection the cable in relation to the platform base.

Analyzing the top view (looking from top to bottom), it can be seen that the length P is made up of two segments.

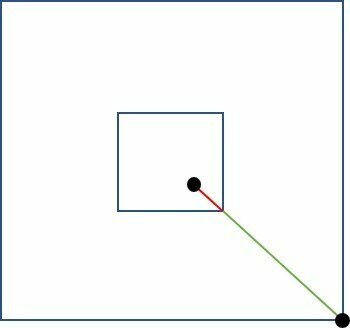
The black dots represent cable attachments.

To determine the segment p, we start by calculating the diagonal of the larger square, which is the platform.

For this, we use the Pythagorean theorem.

We can discard half of the diagonal.

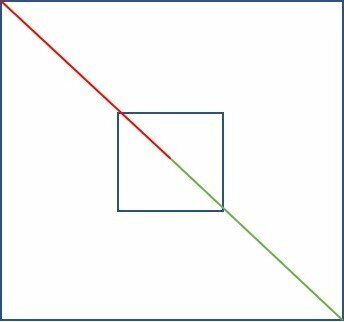
38 / 2 = 19 m

Now we discard another 1/4 of the diagonal of the inner square, which represents the rook.

The highlighted points in the last figure are the ends of the cable and p, the projection of the cable over the platform floor.

To calculate the diagonal of the inner square, we use the Pythagorean theorem.

Soon,

Thus, the measure of the projection is:

Step 3: Cable length calculation c

Returning to the initial figure, we determine p using the Pythagorean theorem.

Conclusion

each cable measures  m. This is how the answer is presented. It can also be said that each cable measures 20 m.

Question 39

Estimating the number of individuals in an animal population often involves capturing, tagging, and then releasing some of these individuals. After a period, after the marked individuals mix with the unmarked ones, another sampling is performed. The proportion of individuals from this second sample that was already marked can be used to estimate the size of the population, applying the formula:

Where:

n1= number of individuals marked in the first sampling;

n2= number of individuals marked in the second sampling;

m2= number of individuals from the second sampling that were tagged in the first sampling;

N= estimated size of the total population.

SADAVA, D. et al. Life: the science of biology. Porto Alegre: Artmed, 2010 (adapted).

During a count of individuals from a population, 120 were marked in the first sampling; in the second sampling, 150 were marked, of which 100 already had the marking.

The estimated number of individuals in this population is

The) 188.

B) 180.

ç) 125.

d) 96.

and) 80.

feedback explained

objective
Determine the number of individuals N.

Data
n1 = 120
n2 = 150
m2 = 100

Substituting into the formula, we have:

Isolating N

question 40

A couple and their two children left, with a realtor, with the intention of buying a lot where they would build their house in the future. In the house project, which this family has in mind, they will need an area of ​​at least 400 m². After some evaluations, they decided between lots 1 and 2 in the figure, in the form of parallelograms, whose prices are R$ 100,000.00 and R$ 150,000.00, respectively.

Use √3/2, 1/2 and 1.7 as approximations, respectively, for sin (60°), cos (60°) and √3 .

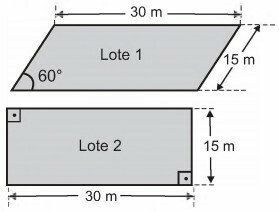
To collaborate in the decision, those involved made the following arguments:

Father: We should buy Lot 1, because as one of its diagonals is larger than the diagonals of Lot 2, Lot 1 will also have a larger area;

Mother: If we disregard the prices, we can buy any lot to execute our project, since both having the same perimeter, they will also have the same area;

Son 1: We should buy Lot 2, as it is the only one that has enough area to carry out the project;

Child 2: We should buy Lot 1, because as the two lots have sides of the same measure, they will also have the same area, but Lot 1 is cheaper;

Broker: You should buy Lot 2, as it has the lowest cost per square meter.

The person who correctly argued for the purchase of the land was (a)

The) dad.

B) mother.

ç) child1.

d) son 2.

and) broker.

feedback explained

The project requires at least 400 m².

Calculation of areas

lot 2

Area = 30 x 15 = 450 m²

lot 1

We have that the base is 30 m and the height can be determined using the sine of 60º.

Using the value of = 1.7, given by the question:

The area of ​​lot 1 is:

About the arguments:.

Child 1 is correct.

Regarding the broker, in any case, lot 1 does not satisfy the project. Still:

lot 1

lot 2

Lot 2 has the highest cost per square meter.

Father: WRONG. The area is not determined by the diagonal.

Mother: WRONG. The area is not determined by the perimeter.

Child 2: WRONG. The area is not determined by just measuring the sides in different ways.

Question 41

Consider that an archeology professor has obtained resources to visit 5 museums, 3 of them in Brazil and 2 outside the country. He decided to restrict his choice to the national and international museums listed in the following table.

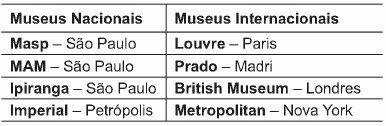
According to the resources obtained, in how many different ways can this teacher choose the 5 museums to visit?

The) 6

B) 8

ç) 20

d) 24

and) 36

feedback explained

There are four national and four international.

Five will be visited in total, 3 national and 2 international.

How many ways can you choose 3 options out of 4 and 2 options out of 4?

By the fundamental principle of counting:

3 options out of 4. 2 options out of 4

It is a combination for nationals and internationals.

For national museums:

For international museums:

Making the product, we have:

6. 4 = 24 options

Question 42

A confectioner wants to make a cake whose recipe calls for the use of sugar and wheat flour in amounts given in grams. He knows that a particular cup used to measure the ingredients holds 120 grams of wheat flour and that three of those cups of sugar correspond, in grams, to four of wheat.

How many grams of sugar fit in one of these cups?

The) 30

B) 40

ç) 90

d) 160 

and) 360

feedback explained

1 cup of wheat = 120g

3 cups of sugar = 4 cups of wheat
3 cups of sugar = 4. 120
3 cups of sugar = 480

So, 1 cup of sugar = 480 / 3 = 160g

Question 43

Taxi service charging systems in cities A and B are different. A taxi ride in city A is calculated at the fixed fare, which is BRL 3.45, plus BRL 2.05 per kilometer driven. In city B, the race is calculated by the fixed value of the flag, which is R$ 3.60, plus R$ 1.90 per kilometer traveled.

One person used the taxi service in both cities to cover the same distance of 6 km.

What value is closest to the difference, in reais, between the average cost per kilometer traveled at the end of the two races?

The) 0,75

B) 0,45

ç) 0,38

d) 0,33

and) 0,13 

feedback explained

Data
6 km traveled in both cities.

Total cost in city A
A = 3.45 + 2.05. 6 = 15,75

Cost per km in city A (average per km)
15,75 / 6 = 2,625

Total cost in city B
B = 3.60 + 1.90. 6 = 15

Cost per km in city B (average per km)
15 / 6 = 2,5

Difference between the averages
2,625 - 2,5 = 0,125

The closest answer is letter e) 0.13.

Question 44

In a 2012 soccer championship, a team was crowned champion with a total of 77 points (P) in 38 games, having 22 wins (W), 11 draws (L) and 5 losses (D). In the criterion adopted for this year, only wins and ties have positive and integer scores. Losses have a value of zero and the value of each win is greater than the value of each draw.

A fan, considering the formula of the unfair sum of points, proposed to the organizers of the championship that, for the year 2013, the team defeated in each match loses 2 points, favoring the teams that lose less throughout the championship. Every win and every draw would continue with the same 2012 score.

What expression gives the number of points (P), as a function of the number of wins (V), the number of draws (E) and the number of defeats (D), in the scoring system proposed by the fan for the year 2013?

The) P = 3V + E

B) P = 3V - 2D

ç) P = 3V + E - D

d) P = 3V + E - 2D 

and) P = 3V + E + 2D

feedback explained

objective
Determine the amount of points P as a function of the number of victories V, defeats D and ties E, according to the criterion suggested by the fan.

Data
Initially:

• Wins and ties are positive.
• Victory is worth more than a draw.
• Losses are worth 0.

fan suggestion

• Loss loses 2 points and win and draw remain the same.

Resolution

Initially the function should be:

P = xV + yE - 2D 

The term -2D refers to the loss of 2 points for each defeat.

It remains to identify the coefficients: x for wins and y for ties.

By elimination, only options b) and d) remain.

As in option b) the term E does not appear, it means that its coefficient is zero 0. But the rule says they must be positive, therefore non-zero.

Thus, only option d) P = 3V + E - 2D remains.

Question 45

A laboratory performed a test to calculate the reproduction speed of a type of bacteria. To do so, he carried out an experiment to observe the reproduction of an amount x of these bacteria for a period of two hours. After this period, there was a population of 189,440 of the aforementioned bacterium in the experiment cabin. Thus, it was found that the population of bacteria doubled every 0.25 hours.
The initial amount of bacteria was

The) 370.

B) 740.

ç) 1 480.

d) 11 840.

and) 23 680.

feedback explained

objective 
Determine the initial quantity x.

Data
Evolution for two hours.
Doubles every 0.25h
Final population = 189 440

Resolution
0.25h = 15 min

2h = 120 min

120/15 = 8

This means that the population doubles eight times.

Home x

1st fold: 2x
2nd fold: 4x
3rd fold: 8x
4th fold: 16x
5th fold: 32x
6th fold: 64x
7th fold: 128x
8th fold: 256x

256x = 189 440

x = 189 440/256
x = 740

Time left3h 00min 00s

hits

40/50

40 correct

7 wrong

3 unanswered

hit on 40 questions from a total of 50 = 80% (percentage of correct answers)

Simulation time: 1 hour and 33 minutes

Questions(click to go back to the question and check the feedback)

answeredunanswered

Missing 8 questions for you to finish.

Heads up!

Do you want to end the simulation?

Noend simulationYea