THE electrical force is the force that arises when there are two electric charges interacting with each other's electric fields. We calculate its intensity using the Coulomb's law.
Its direction is according to the imaginary line joining the charges, and its direction varies according to the signs of the electric charges. So when \(q\geq0\), the direction between the forces is attractive. But when \(q<0\), the direction between the forces is repulsive.
Coulomb's law, in addition to being used in the calculation of force, interconnects this electrostatic force with the squared distance between the charges and the environment in which they are inserted. The work of the electric force can be found by the amount of energy that the electrical charge need to get from one place to another, regardless of the route chosen.
Read too: How does the movement of electrical charges work?
Electric power summary
Electric force deals with the interaction between electric charges.
The direction of the electric force is the same as the imaginary line connecting the electric charges. attractive or repulsive depending on the signs of the charges, and its intensity is calculated by the law of Coulomb.
Coulomb's law associates the magnitude of the electric force with the distance between two electric charges.
Electric charges of like signs attract each other. Charges with opposite signs repel each other.
Work can be calculated by the “effort” that an electric charge makes to move from one point to another.
Do not stop now... There's more after the ad ;)
What is and what is the origin of electric force?
The electrostatic force, commonly called the electrical force, is part of the four fundamental interactions of the universe, along with the strong nuclear, weak nuclear and gravitational forces. It appears whenever there is an electric field with an electric charge inside it.
The orientation of the electrical force is as follows:
Direction: parallel to the imaginary line connecting the electric charges.
Sense: attractive if the charges have the same sign or repulsive if the charges have opposite signs.
Intensity: calculated by Coulomb's law.
Coulomb's Law
Coulomb's law is the physical principle responsible for the association between the electrostatic force and the distance between two electric charges immersed in the same medium. It was developed by Charles-Augustin de Coulomb (1736‒1806) in 1785.
There is a proportionality relationship between force and loads, but the force is inversely proportional to the square of the distance, that is, if we double the distance, the force decreases \(\frac{1}{4}\) of its original value.
\(\vec{F}\propto\left| Q_1\right|\ e\left| Q_2\right|\)
\(\vec{F}\propto\frac{1}{d^2}\)
It is worth mentioning the importance that the sign of the electric charges has in determining the direction of the force acting between them, being attractive for charges with opposite signs and repulsive when the charges have opposite signs. equals.
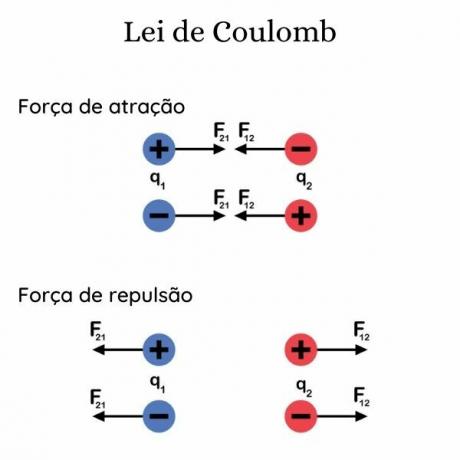
Coulomb's law formula is represented by:
\(\vec{F}=k\frac{\left| Q_1\right|\ \bullet\left| Q_2\right|}{d^2}\)
\(\vec{F}\) is the force of interaction between electrically charged particles, measured in Newton [N].
\(\left| Q_1\right|\) and \(\left| Q_2\right|\) are the charge modules of the particles, measured in Coulomb \([Ç]\).
d is the distance between the charges, measured in meters [m].
k is the electrostatic constant of the medium, measured in \({\left (N\bullet m\right)^2/C}^2\).
Observation: The electrostatic constant changes according to the environment the charges are in.
→ Video lesson on Coulomb's law
electrical force work
Work is the application of a force for a displacement, and it is irrelevant which path was taken, as long as they start from the same point towards the same place.
In view of this, the electrical force workdepends on the force applied to an electric charge to cross the distance from point 1 to point 2, as shown in the image.

We calculate the work using the formula:
\(W=\vec{F}\bullet d\bullet\cos{\theta}\)
W is work, measured in joules \([J]\).
d is the displaced distance, measured in meters \([m]\).
θ is the angle between \(\vec{F}e\ d,\), measured in degrees.
Read too: Electrostatics — area of Physics intended for the study of charges at rest
Electric force and electric field
THE electric field occurs in the vicinity of an electric charge or an electrified surface, being an intrinsic property of charges. THE Electric force arises when there is interaction between electric fields of at least two electrical charges, as shown in the image.

Regarding the orientation of the electric field with respect to the electric force:
Direction: the same as the electric force, that is, parallel to the line joining the electric charges.
Sense: the same of the force if \(q\geq0\), but opposite to the force if \(q<0\).
Intensity: calculated by the electric field formula or by the formula that relates electric force and electric field, described below:
\(\vec{F}=\left|q\right|\bullet\vec{E}\)
q is the electric charge, measured in coulombs \([Ç]\).
\(\vec{E}\) is the electric field, measured in \([N/C]\).
→ Video lesson on electric field
Exercises solved on electrical force
question 1
(Mack-SP) A point electric charge with \(q=4.0\ \mu C\), which is placed at a point P in the vacuum, is subjected to an electric force of magnitude \(1.2\ N\). The electric field at that point P has magnitude:
The) \(3.0\bullet{10}^5\ N/C\)
B) \(2.4\bullet{10}^5\ N/C\)
ç) \(1,2\bullet{10}^5\ N/C\)
d) \(4.0\bullet{10}^{-6}\ N/C\)
and) \(4.8\bullet{10}^{-6}\ N/C\)
Resolution:
Alternative A
As in the statement the force value is provided and the field is requested, we can use the form that relates both:
\(\vec{F}=\left|q\right|\bullet\vec{E}\)
\(1,2=\left|4,0\ \mu\right|\bullet\vec{E}\)
Remembering that \(\mu={10}^{-6}\), we have:
\(1,2=4,0\bullet{10}^{-6}\bullet\vec{E}\)
\(\frac{1,2}{4,0\bullet{10}^{-6}}=\vec{E}\)
\(0.3\bullet{10}^6=\vec{E}\)
\(3\bullet{10}^{-1}\bullet{10}^6=\vec{E}\)
\(3\bullet{10}^{-1+6}=\vec{E}\)
\(3\bullet{10}^5N/C=\vec{E}\)
question 2
There is an electrical charge of \(2.4\bullet{10}^{-4}\ C\) in an electric field of \(6\bullet{10}^4\N/C\) which moves 50 cm parallel to the field axis. What work does the load do?
The)\(W=-7.2\ J\)
B)\(W=14.4\bullet{10}^{-2}\ J\)
ç)\(W=7.2\bullet{10}^{-2}\ J\)
d)\(W=14.4\ J\)
and) \(W=7.2\ J\)
Resolution:
Alternative E
Using the formula relating work and electric force:
\(W=\vec{F}\bullet d\bullet\cos{\theta}\)
Since the electric force was not given, we can do the calculation using the electric field and the charge. Remembering that since the charge is positive, its force and field are in the same direction, so the angle between the force and the displaced distance is 0°:
\(W=\left|q\right|\bullet\vec{E}\bullet d\bullet\cos{\theta}\)
\(W=\left|2,4\bullet{10}^{-4}\right|\bullet\left (6\bullet{10}^4\right)\bullet0,5\bullet\cos0°\)
\(W=14.4\bullet{10}^{-4+4}\bullet0.5\bullet1\)
\(W=14.4\bullet0.5\)
\(W=7.2\ J\)
By Pâmella Raphaella Melo
Physics teacher
