THE Kepler's second law, also known as the law of areas, was created by Johannes Kepler to explain the exotic orbit of Mars that had been observed. This law describes that a body orbiting another, the latter in a frame of rest, will cover equal areas in equal time intervals.
The main consequence of this law is the variation that occurs in orbital velocity, because when the planet is at perihelion, that is, closer to the Sun, it will have greater speed, but if it is at aphelion, that is, farther from the Sun, it will have speed smaller.
Read too: Three common mistakes made in the study of universal gravitation
Summary of Kepler's second law
Johannes Kepler was the physicist responsible for the study and the observations contained in the three Kepler's laws.
Kepler's laws were developed based on Johannes Kepler's findings about the orbit of Mars.
Orbits around the Sun describe elliptical paths, in which the Sun is at one of the foci of the ellipse.
Kepler's second law describes that bodies orbiting another body at rest make equal area displacements in equal time intervals.
This law is a consequence of the principle of conservation of angular momentum.
The orbital velocity of the planet at perihelion is greater than at aphelion.
Do not stop now... There's more after the ad ;)
What does Kepler's second law say?
Based on observations and evidence regarding the eccentric orbit of Mars, which described an elliptical motion and with orbital velocities varying according to its approach and departure from theSun, Johannes Kepler (1571-1630) developed his second law, also called the law of areas.
The statement of Kepler's second law reads as follows:
“The radius vector connecting a planet to the Sun describes equal areas in equal times.”

Using the figure as an example, the law tells us that the time to go through area 1 will be the same for area 2, as long as these areas are the same, even if they appear to be of different sizes.
As a result, the orbital velocity undergoes changes, in which, if the body is closer to the Sun (perihelion), the velocity will be greater, but if it is further away (aphelion), it will be smaller.
VPerihelion > Vaphelion
It is worth mentioning that Kepler's laws do not only work for the orbits of planets around the Sun, but also for any body orbiting another that is at rest and when the interaction between them is gravitational.
As an example we have the natural satellites, such as the Moon, which orbits around the Earth, and the moons of Saturn, which orbit around this planet, following these laws. In these cases, Earth and Saturn are the references at rest respectively.
Read too: What would happen if the Earth stopped rotating?
Kepler's second law formula
The formula that describes Kepler's second law is:
\(\frac {A_1}{∆t_1}=\frac{A_2}{∆t_2}\)
\(TO 1\ \)and \(A_2\)are the areas comprised by the movement, measured in .
\(∆t_1\)and \(∆t_2 \)are the changes in time that occur in the displacement, measured in seconds.
How to apply Kepler's second law?
Kepler's second law is used whenever working with displacements of celestial bodies with equal areas and, consequently, in equal time intervals.
Thus, it can be used in the study of the movement of the planets around the Sun or other stars; of natural and artificial satellites around the planets, among others.
Video lesson on Kepler's laws
Solved exercises on Kepler's second law
Question 01
(Unesp) Analyze the movement of a planet at different points in its trajectory around the Sun, as shown in figure A. Considering the stretches between points A and B and between points C and D, it can be said that,
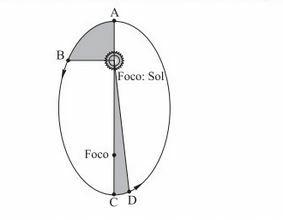
(A) Between A and B, the area swept by the line connecting the planet to the Sun is greater than that between C and D.
(B) if the shaded areas are equal, the planet moves with greater speed in the stretch between A and B.
(C) if the shaded areas are equal, the planet moves with greater speed in the stretch between C and D.
(D) if the shaded areas are equal, the planet moves with the same speed in both sections.
(E) if the shaded areas are equal, the time taken for the planet to go from A to B is longer than between C and D.
Resolution:
Alternative B. Assuming that the shaded areas are equal, by Kepler's second law, it can be deduced that the planet will move with a faster at perihelion, when it is closer to the Sun, and slower at aphelion, when it is further away from the Sun. Sun. So, in the interval AB, it will have higher speed.
question 2
(Unesp) The orbit of a planet is elliptical and the Sun occupies one of its foci, as illustrated in the figure (out of scale). The regions bounded by the OPS and MNS contours have areas equal to A.

if \(top\) and \(t_MN\) are the time intervals spent for the planet to traverse the OP and MN sections, respectively, with average speeds \(v_OP\) and \( v_MN\), it can be stated that:
The) \(t_OP>t_MN \) and \(v_OP
B) \( t_OP=t_MN \) and \(v_OP>v_MN\)
ç) \( t_OP=t_MN \) and \(v_OP
d) \(t_OP>t_MN\) and \(v_OP>v_MN\)
and)\( t_OP and \(v_OP
Resolution:
Alternative B. According to Kepler's second law, the regions bounded by the OPS and MNS boundaries occur at equal time intervals, so \(t_OP=t_MN\). Also, the velocity at perihelion will be greater than at aphelion, so \(v_OP>v_MN\).
By Pâmella Raphaella Melo
Physics teacher



