O cylinder it is a geometric solid quite common in everyday life, as it is possible to identify various objects that have the shape of it, such as a pencil, certain packages, oxygen cylinders, among others. There are two types of cylinder: the straight cylinder and the oblique cylinder.
The cylinder is formed by two circular bases and lateral area. Because it has a circular base, it is classified as a round body. To calculate the base area, side area, total area and volume of the cylinder, we use specific formulas. The cylinder's unfolding is composed of two circles, which are its bases, and a rectangle, which is its side area.
See too: Cone — what is it, elements, classification, area, volume
cylinder summary
- It is a geometric solid classified as a round body.
- It consists of two circular bases and its lateral area.
- To calculate the area of your base, the formula is:
\(A_b=\pi r^2\)
- To calculate its lateral area, the formula is:
\(A_l=2\pi rh\)
- To calculate its total area, the formula is:
\(A_T=2\pi r^2+2\pi rh\)
- To calculate its volume, the formula is:
\(V=\pi r^2\cdot h\)
What are the cylinder elements?
The cylinder is a geometric solid that has two bases and a side area. Its bases are formed by two circles, which contributes to the fact that the cylinder is a round body. Its main elements are the two bases, the height, the lateral area and the radius of the base. See below:

What are the types of cylinder?
There are two types of cylinder: straight and oblique.
straight cylinder
When the axis is perpendicular to the bases.

oblique cylinder
When he is inclined.

cylinder planning
THE flattening of geometric solids is the representation of its faces in a planar form. The cylinder is composed of two bases that are shaped like a circle, and its lateral area is a rectangle, as shown in the figure:
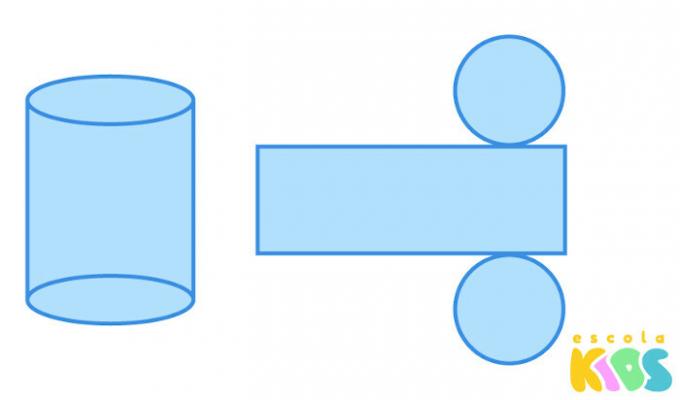
What are the cylinder formulas?
There are important calculations involving cylinder, they are: base area, lateral area, total area and volume area. Each of them has a specific formula.
Cylinder base area
As we know, the base of a cylinder is formed by a circle, so, to calculate its base area, we use the formula of area of a circle:
\(A_b=\pi r^2\)
- Example:
Find the area of the base of a cylinder that has a radius of 8 cm.
(Use \(π=3,14\))
Resolution:
Calculating the area of the base, we have:
\(A_b=\pi r^2\)
\(A_b=3.14\cdot8^2\)
\(A_b=3.14\cdot64\)
\(A_b=200.96\ cm^2\)
Read too: How to calculate the area of the triangle?
Cylinder side area
The lateral area of the cylinder is a rectangle, but we know that it surrounds the circle of the base, so one of its sides measures the same as the length of the cylinder. circumference, so its area is equal to product between the length of the circumference of the base and the height. The formula to calculate the lateral area is:
\(A_l=2\pi r\cdot h\)
- Example:
Calculate the lateral area of a cylinder whose height is 6 cm, radius is 2 cm, and π=3,1.
Resolution:
Calculating the lateral area, we have:
\(A_l=2\cdot3,1\cdot2\cdot6\)
\(A_l=6.1\cdot12\)
\(A_l=73.2\ cm²\)
total cylinder area
The total area of a cylinder is nothing but the sum of the area of your two bases with the lateral area:
\(A_T=A_l+2A_b\)
So we have to:
\(A_T=2\pi rh+2\pi r^2\)
- Example:
Calculate the total area of a cylinder that has r = 8 cm, height 10 cm, and using \(π=3\).
Resolution:
\(A_T=2\cdot3\cdot8\cdot10+2\cdot3\cdot8^2\)
\(A_T=380+6\cdot64\)
\(A_T=380+384\)
\(A_T=764\)
Cylinder area video
cylinder volume
Volume is a very important quantity for geometric solids, and the cylinder volume is equal to product between the area of the base and the height, so the volume is given by:
\(V=\pi r^2\cdot h\)
- Example:
What is the volume of a cylinder that has a radius of 5 cm and a height of 12 cm? (Use \(π=3\))
Resolution:
Calculating the volume of the cylinder, we have:
\(V=3\cdot5^2\cdot12\)
\(V=\ 3\ \cdot25\ \cdot12\)
\(V=900\ cm^3\ \)
Cylinder volume video
Solved exercises on cylinder
question 1
The packaging of a given product has a base of 10 cm in diameter and a height of 18 cm. So the volume of this package is:
(Use \(π = 3\))
A) 875 cm³
B) 950 cm³
C) 1210 cm³
D) 1350 cm³
E) 1500 cm³
Resolution:
Alternative D
We know that the radius is equal to half the diameter, so:
r = 10: 2 = 5 cm
Calculating the volume, we have:
\(V=\pi r^2\cdot h\)
\(V=3\cdot5^2\cdot18\)
\(V=\ 3\cdot25\cdot18\)
\(V=\ 75\cdot18\ \)
\(V=1350\ cm³\)
question 2
(USF-SP) A right circular cylinder, of volume 20π cm³, has a height of 5 cm. Its lateral area, in square centimeters, is equal to:
A) 10π
B) 12π
C) 15π
D) 18π
E) 20π
Resolution:
Alternative E
We know that:
\(V = 20\pi cm³\)
\(h = 5 cm\)
The lateral area is given by:
\(A_l=2\pi rh\)
So, to find r, we have to:
\(V=\pi r^2\cdot h\)
\(20\pi=\pi r^2\cdot5\)
\(\frac{20\pi}{5\pi}=r^2\)
\(r^2=4\)
\(r=\sqrt4\)
\(r\ =\ 2\)
Knowing that r = 2, then we will calculate the lateral area:
\(A_l=2\pi rh\)
\(A_l=2\pi\cdot2\ \cdot5\)
\(A_l=20\pi\)



