THE ball is a geometric solid classified as a round body due to its rounded shape. We can define it as the set of points in space that are the same distance from its center. This distance is an important element of the sphere, known as the radius.
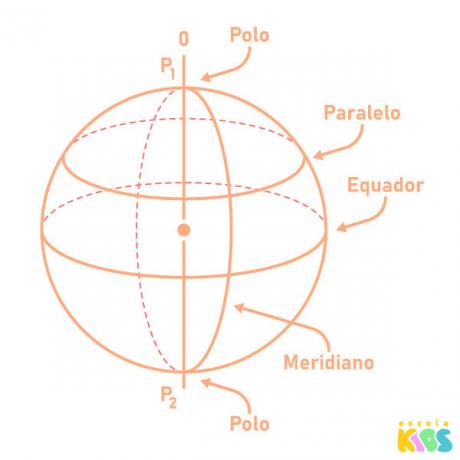
Some parts of the sphere are given special names, such as the equator, poles, parallels, and meridians. To calculate the total area and volume of the sphere, there are specific formulas.
Read too: Difference between circumference, circle and sphere
Summary about the sphere
The sphere is a geometric solid classified as a round body.
The main elements of the sphere are its origin and its radius.
The total area of the sphere is calculated by the formula:
\(A=4\pi r^2\)
The volume of the sphere is calculated by the formula:
\(V=\frac{4}{3}\pi r^3\)
Identifying the elements of the sphere
There are two fundamental elements of the sphere, which are the center and radius. When we define them, we have that the sphere is the set formed by all points that are at a distance equal to or less than the length of the radius.
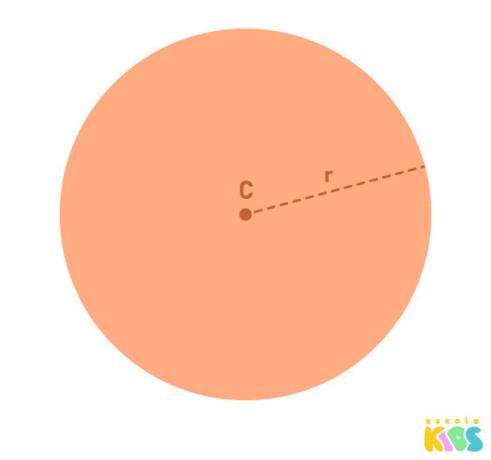
C ➔ center or origin of the sphere.
r ➔ radius of the sphere.
In addition to the elements listed above, there are others, which are given specific names. There are the poles, meridians, parallels and the equator.
Calculating the area of the sphere
The area of a geometric solid is the measurement of the surface of this solid. We can calculate the area of the sphere using the formula:
\(A=4\pi r^2\)
Example:
A sphere has a radius of 12 cm. using \(\pi=\ 3,14,\) Calculate the area of this sphere.
Resolution:
Calculating the area, we have:
\(A=4\pi r^2\)
\(A=4\cdot3,14\cdot{12}^2\)
\(A=4\cdot3,14\cdot144\)
\(A=1808.64\ cm²\)
Video lesson on the sphere area
Calculation of the volume of the sphere
Volume is another important quantity in geometric solids. To calculate the volume of the sphere, we use the formula:
\(V=\frac{4}{3}\pi r^3\)
Therefore, it is enough to know the value of the radius to calculate the volume of the sphere.
Example:
A sphere has a radius of 2 meters. Knowing that \(\pi=3\), find the volume of this sphere.
Resolution:
\(V=\frac{4}{3}\pi r^3\)
\(V=\frac{4}{3}\cdot3\cdot2^3\)
\(V=4\cdot2^3\)
\(V=4\cdot8\)
\(V=32\ m³\)
Video lesson on sphere volume
What are the parts of the sphere?
There are parts of the sphere that are given specific names, such as the spherical spindle, the spherical wedge, and the hemisphere.
spherical spindle: part of the surface of the sphere.
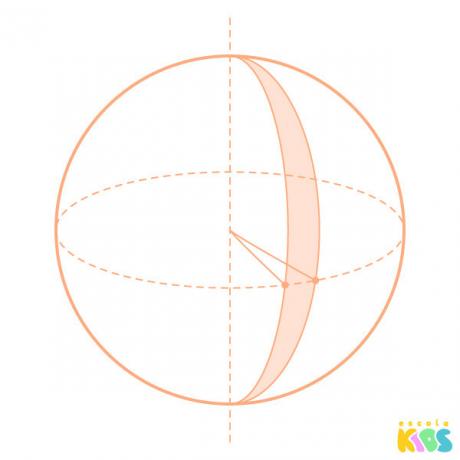
spherical wedge: geometric solid formed by the part of the sphere that goes from the spindle to the origin, like a slice.

Hemisphere: nothing more than half a sphere.

Read too: Circumference — plane figure constructed by the set of points that are the same distance from the center
Solved exercises on sphere
question 1
Pilates is a set of exercises that help in the development and restoration of health. In the practice of these exercises, it is common to use a gym ball. In a rehabilitation center that promotes Pilates classes, a ball is 60 cm in diameter. Analyzing this ball, we can say that its surface area is:
A) 3600 \(\pi\)
B) 2700\(\pi\)
C) 2500\(\pi\)
D) 1700\(\pi\)
E) 900\(\pi\)
Resolution:
Alternative A
We know that the surface area is calculated by:
\(A=4\pi r^2\)
If the diameter is 60 cm, the radius will be 30 cm:
\(A=4\cdot\pi\cdot{30}^2\)
\(A=4\cdot\pi\cdot900\)
\(A=3600\pi cm²\)
question 2
Seeking to innovate in the packaging of its perfumes, a company decided to develop containers that have a sphere shape, with a radius of 5 cm. using \(\pi=3\), the volume of one of these containers, in cm³, is:
A) 250 cm³
B) 500 cm³
C) 750 cm³
D) 1000 cm³
Resolution:
Alternative B
Calculating the volume:
\(V=\frac{4}{3}\pi r^3\)
\(V=\frac{4}{3}\cdot3\cdot5^3\)
\(V=4\ \cdot125\ \)
\(V=500cm^3\)



