The factorization of polynomials consists of methods developed to rewrite a polynomial as a product between polynomials. Write the polynomial as the multiplication between two or more factors helps in simplifying algebraic expressions and understanding a polynomial.
There are different cases of factoring, and for each of them there are specific techniques.. The existing cases are: factoring by common factor in evidence, factoring by grouping, difference between two squares, perfect square trinomial, sum of two cubes and difference of two cubes.
Read more:What is polynomial?
Summary on factoring polynomials
Factorization of polynomials are techniques used to represent the polynomial as a product between polynomials.
We use this factorization to simplify algebraic expressions.
-
The factoring cases are:
Factoring by common factor in evidence;
Factoring by grouping;
perfect square trinomial;
difference of two squares;
sum of two cubes;
Difference of two cubes.
Polynomial Factoring Cases
To factor a polynomial,
it is necessary to analyze in which of the factoring cases the situation fits, being: factoring by common factor in evidence, factoring by grouping, difference between two squares, perfect square trinomial, sum of two cubes and difference of two cubes. Let's see how to perform the factorization in each of them.Do not stop now... There's more after the ad ;)
Common factor in evidence
We use this factoring method when there is a factor common to all terms of the polynomial. This common factor will be highlighted as one factor, and the other factor, the result of the division of the terms by that common factor, will be placed inside the parentheses.
Example 1:
20xy + 12x² + 8xy²
Analyzing each term of this polynomial, it is possible to see that x is repeated in all terms. Also, all coefficients (20, 12, and 8) are multiples of 4, so the factor common to all terms is 4x.
Dividing each term by the common factor, we have:
20xy: 4x = 5y
12x²: 4x = 3x
8xy²: 4x = 2y²
Now, we will write the factorization putting the common factor in evidence and the sum of the results found in parentheses:
4x (5y + 3x + 2y²)
Example 2:
2a²b² + 3a³b – 4a5b³
Analyzing the literal part of each term, it is possible to see that a²b is repeated in all of them. Note that there is no number that divides 2, 3 and – 4 at the same time. So the common factor will be just a²b.
2a²b²: a²b = 2b
3a³b: a²b = 3a
4th5b³: a²b = 4a³
Thus, the factorization of this polynomial will be:
a²b (2b + 3a + 4a³)
See too: Addition, subtraction and multiplication of polynomials — understand how they are done
grouping
This method is used when there is no common factor for all terms of the polynomial. In this case, we identify terms that can be grouped having a common factor and highlight them.
Example:
Factor the following polynomial:
ax + 4b + bx + 4a
We will group the terms that have a and b as a common factor:
ax + 4a + bx + 4b
Putting a and b in evidence in terms of two by two, we have:
a(x+4)+b(x+4)
Note that inside the parentheses the factors are the same, so we can rewrite this polynomial as:
(a + b) (x + 4)
perfect square trinomial
Trinomials are polynomials with 3 terms. A polynomial is known as a perfect square trinomial when it is sum squared or difference squared result, that is:
a² + 2ab + b² = (a + b) ²
a² – 2ab + b² = (a – b) ²
Important: Not every time there are three terms this polynomial will be a perfect square trinomial. Therefore, before carrying out the factorization, it must be verified if the trinomial fits in this case.
Example:
Factor, if possible, the polynomial
x² + 10x + 25
After analyzing this trinomial, we will extract the square root first and last term:
\(\sqrt{x^2}=x\)
\(\sqrt{25}=5\)
It is important to verify that the central term, that is, 10x, is equal to \(2\cdot\ x\cdot5\). Note that it is indeed the same. So this is a perfect square trinomial, which can be factored by:
x² + 10x + 25 = (x + 5)²
difference of two squares
When we have a difference of two squares, we can factor this polynomial by rewriting it as the product of the sum and the difference.
Example:
Factor the polynomial:
4x² – 36y²
First, we will calculate the square root of each of its terms:
\(\sqrt{4x^2}=2x\)
\(\sqrt{36y^2}=6y\)
Now, we will rewrite this polynomial as the product of the sum and difference of the roots found:
4x² – 36y² = (2x + 6y) (2x – 6y)
Read too: Algebraic calculation involving monomials — learn how the four operations occur
sum of two cubes
The sum of two cubes, that is, a³ + b³, can be factored as:
a³ + b³ = (a + b) (a² – ab + b²)
Example:
Factor the polynomial:
x³ + 8
We know that 8 = 2³, so:
x³ + 8 = (x + 2) (x² - 2x + 2²)
x³ + 8 = (x + 2) (x² - 2x + 4)
Difference of two cubes
The difference of two cubes, that is, a³ – b³, not unlike the sum of two cubes, can be factored as:
a³ – b³ = (a – b) (a² + ab + b²)
Example:
Factor out the polynomial
8x³ - 27
We know that:
8x³ = (2x) ³
27 = 3³
So we have to:
\(8x^3-27=\left (2x-3\right)\)
\(8x^3-27=\left (2x-3\right)\left (4x^2+6x+9\right)\)
Solved exercises on factoring polynomials
question 1
Using Polynomial Factorization to Simplify Algebraic Expression \(\frac{x^2+4x+4}{x^2-4},\), we will find:
a) x + 2
B) x - 2
Ç) \(\frac{x-2}{x+2}\)
D) \(\frac{x+2}{x-2}\)
E) (x - 2) (x + 2)
Resolution:
Alternative D
Looking at the numerator, we see that x² + 4x + 4 is a case of a perfect square trinomial and can be rewritten as:
x² + 4x + 4 = (x + 2)²
The numerator x² – 4 is the difference of two squares and can be rewritten as:
x² - 4 = (x + 2) (x - 2)
Therefore:
\(\frac{\left (x+2\right)^2}{\left (x+2\right)\left (x-2\right)}\)
Note that the term x + 2 appears both in the numerator and in the denominator, so its simplification is given by:
\(\frac{x+2}{x-2}\)
question 2
(Unifil Institute) Considering that two numbers, x and y, are such that x + y = 9 and x² – y² = 27, the value of x is equal to:
a) 4
B) 5
C) 6
D) 7
Resolution:
Alternative C
Note that x² – y² is the difference between two squares and can be factored as the product of the sum and the difference:
x² – y² = (x + y) (x – y)
We know that x + y = 9:
(x + y) (x - y) = 27
9 (x - y) = 27
x - y = 27: 9
x - y = 3
Then we can set up a equation system:
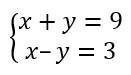
Adding the two lines:
2x + 0 y = 12
2x = 12
x = \(\frac{12}{2}\)
x = 6
By Raul Rodrigues de Oliveira
Maths teacher
