Study temperature and heat with the list of exercises on: setting temperature and heat, expansion and thermal equilibrium, thermometric scales, heat transfer, latent and sensible heat. There are several solved and commented exercises for you to learn and solve your doubts.
Exercises on setting Temperature and Heat
Exercise 1
Define and differentiate temperature and heat.
Temperature is a measure of the thermal state of a physical body or system. It determines the degree of agitation of the particles that make up this system.
Temperature is therefore a quantity, something that can be measured. In the International System of Units, the unit of measurement for temperature is the Kelvin (K). Other common units are Celsius (°C) and Fahrenheit (°F).
Heat is the movement of thermal energy. Thermal energy is transferred from more energetic bodies, with a higher temperature, to less energetic bodies and systems, with a lower temperature. This energy transfer takes place through processes such as: conduction, convection and irradiation.
Since heat is a form of energy, in the International System of Units it is measured in joules (J). Another common measure for heat is calorie (lime).
The main difference between temperature and heat is that temperature is a measure of the thermal state while heat is the transfer of thermal energy between bodies.
Exercise 2
Define what is thermal equilibrium.
Thermal equilibrium is the state in which different bodies in the same environment are at the same temperature, that is, they have the same thermal state.
Since heat is the transfer of thermal energy from warmer bodies to cooler ones, previously hotter bodies cool as they give off heat. On the other hand, bodies that receive this heat, which were colder before, become warm.
This temperature variation ceases when there is no more heat between the bodies, which means that there is no more transfer of thermal energy between them. In this state, their temperatures are the same.
Exercise 3
Explain the following phenomenon:
Laura has just woken up and got out of bed on a cold winter's day. After getting out of her warm bed, she touches her feet to the carpeted floor of her bedroom and feels comfortable, even in her bare feet. When you go into the kitchen, your bare feet feel a cold sensation when touching the tile floor.
The entire environment of the house was exposed to the same temperature conditions throughout the night. Why does Laura feel different sensations when walking barefoot in the bedroom and in the kitchen?
The sensations of hot and cold are related to several factors, some even subjective. Different people can feel and perceive the same temperature in different ways. However, in the text, the same person has different sensations in an environment that is supposed to be in thermal equilibrium, that is, where the bodies are at the same temperature.
The only difference is the material it comes into contact with. The thermal conductivity coefficient is a property of materials and indicates how easily thermal energy is transferred. The more the thermal conductivity value, the easier the transfer of thermal energy is.
As ceramic flooring has greater thermal conductivity than wool or cotton carpet, Laura's body loses a lot. more energy when she walks through the kitchen than when she walks across the carpet, which makes her interpret that the floor is more cold.
Exercises on Thermal Equilibrium
Exercise 4
(IFF 2016) In the laboratory activity, the Physics teacher proposes that students mix 1L of water at a temperature of 100°C with 500 mL of water at 4°C. However, before mixing and measuring the thermal equilibrium temperature, students need to calculate the thermal equilibrium temperature. Consider negligible thermal losses and that the theoretical result is equal to the experimental value. It can be said that this equilibrium temperature is valid:
a) 68°C.
b) 74°C.
c) 80°C.
d) 32°C.
e) 52°C.
Correct answer: a) 68°C.
Objective: determine the thermal equilibrium temperature ().
Data:
1L = 1000 ml of water at 100°C;
500 ml of water at 4°C
Physical and Mathematical Model
In thermal equilibrium there is no more transfer of thermal energy, so the sum of the heats of the portions of water at 100°C and 4°C is equal to zero.
Since on both sides of the equation the specific heat is the same, we can cancel them out.
Therefore, the equilibrium temperature will be 68°C.
Exercises on Thermometric Scales
Exercises 5
(SENAC - SP 2013) The arrival of man on the moon happened in 1969. The structure of the moon is rocky and has practically no atmosphere, which means that during the day the temperature reaches 105 °C and at night it drops to −155 °C.
This thermal variation, measured on the Fahrenheit temperature scale, is valid
a) 50.
b) 90.
c) 292.
d) 468.
e) 472.
Correct answer: d) 468.
The relationship between the Celsius °C scale and the °F scale is given by:
Where,
is the temperature variation in degrees Celsius and,
is the variation on Fahrenheit.
The temperature on the lunar surface varies between 105°C and at night -155°C. Therefore, the total variation is 260°C.
105 - (-155) = 260
Substituting in the formula, we have:
Exercises 6
(UESPI 2010) A student is reading the science fiction novel “Fahrenheit 451” by Ray Bradbury. In a certain passage, one of the characters claims that 451 °F is the temperature on the Fahrenheit scale at which the paper from which books are made combust. The student knows that, on this scale, the melting and boiling temperatures of water are 32°F and 212°F, respectively. He rightly concludes that 451°F is roughly equivalent to:
a) 100 °C
b) 205 °C
c) 233 °C
d) 305 °C
e) 316 °C
Correct answer: c) 233 °C.
The Celsius and Fahrenheit scales are related by:
Replacing 451°F with , we have:
Of the response options 233°C is the closest.
Exercises 7
(FATEC 2014) During a Formula Indy or Formula 1 race, drivers are subjected to a hot microenvironment in the cockpit that it reaches 50°C, generated by various heat sources (from the sun, engine, terrain, brain metabolism, muscle activity etc.). This temperature is way above the tolerable average body temperature, so they should always be in good physical condition.
Formula Indy racing is more traditional in the US, where temperature reading is adopted on the Fahrenheit scale. Based on the information presented in the text, it is correct to state that the cockpit temperature that a Formula Indy car reaches during the race, in Fahrenheit degree, is
Data:
Ice melting temperature = 32°F;
Boiling water temperature = 212°F.
a) 32.
b) 50.
c) 82.
d) 122.
e) 212.
Correct answer: d) 122
To relate the two temperatures, we use the equation:
replacing for 50 and solving for
, we have:
Therefore, the temperature in the cockpit in Fahrenheit is 122°F.
Exercises on Heat Propagation
Exercise 8
(Enem 2021) In an instruction manual for a refrigerator, there are the following recommendations:
• Keep your refrigerator door open only as long as necessary;
• It is important not to obstruct air circulation with poor distribution of food on the shelves;
• Leave a space of at least 5 cm between the rear of the product (serpentine heat sink) and the wall.
Based on the principles of thermodynamics, the justifications for these recommendations are, respectively:
a) Reduce the cold output from the refrigerator to the environment, ensure the transmission of cold between the foods on the shelf and allow heat exchange between the heat sink and the environment.
b) Reduce the cold output of the refrigerator to the environment, guarantee the convection of the internal air, guarantee thermal insulation between the internal and external parts.
c) Reduce the heat flow from the environment to the inside of the refrigerator, ensure the convection of the internal air and allow the exchange of heat between the heatsink and the environment.
d) Reduce the heat flow from the environment to the inside of the refrigerator, ensure transmission the cold between the foods on the shelf and allow the exchange of heat between the sink and the environment.
e) Reduce the heat flow from the environment to the inside of the refrigerator, guarantee the convection of the internal air and guarantee thermal insulation between the internal and external parts.
Correct answer: c) Reduce the heat flow from the room to the inside of the refrigerator, ensure the convection of the internal air and allow the heat exchange between the heatsink and the environment.
Keeping the refrigerator door closed, opening only the necessary, prevents the entry of heat from the external environment.
Inside the refrigerator, heat exchanges between the cold indoor environment and the food produce air currents through convection. These currents are necessary for cooling food.
The heat taken from the food and exchanged with the refrigerator's refrigerant is transported to the heatsink at the back. This heat will be exchanged with the environment, mainly by convection, so space is needed.
Exercise 9
(UEPB 2009) A child who liked brigadeiro decided to make this candy, and for that he started to separate the ingredients and utensils. Initially he took the condensed milk can, the powdered chocolate and the margarine, then a steel pan and spoon and a can opener. The child drilled a hole in the can in order to drain the condensed milk into the pan. His mother, seeing that attitude, suggested that the son drill another hole in the can, so that he would be able to remove that liquid more easily. When placing the pot on the fire to stir the brigadeiro, the child felt that, after a few minutes, the handle of the spoon had warmed up and complained: “Mother, the spoon is burning my hand”. So, his mother asked him to use a wooden spoon to prevent a burn.
About the warming of the spoon evidenced in the child's complaint that his hand was burning, we can say that
a) with a wooden spoon, which is an excellent thermal insulator, it heats up faster than a steel spoon.
b) it happens because the particles that make up the spoon create convection currents, heating it completely, from one end to the other.
c) due to irradiation, the spoon heats up completely, from one end to the other.
d) with a wooden spoon, which is an excellent thermal conductor, it heats up faster than a steel spoon.
e) it happens because the particles that make up the spoon start to conduct the heat absorbed there from one end to the other.
Correct answer: e) it happens because the particles that make up the spoon start to conduct the heat absorbed there from one end to the other.
The heat propagation process is conduction. Only energy is transferred from a particle to its surroundings. Metals are excellent heat transmitters.
Exercise 10
(Enem 2016) In an experiment, a teacher leaves two trays of the same mass, one plastic and the other aluminum, on the laboratory table. After a few hours, he asks the students to rate the temperature of the two trays, using touch. His students categorically claim that the aluminum tray is at a lower temperature. Intrigued, he proposes a second activity, in which he places an ice cube on each of the trays, which are in thermal equilibrium with the environment, and asks them at which the rate of ice melt will be larger.
The student who correctly answers the teacher's question will say that the melting will occur
a) faster on the aluminum tray, as it has a higher thermal conductivity than plastic.
b) faster on the plastic tray, as it initially has a higher temperature than the aluminum one.
c) faster on the plastic tray, as it has a higher thermal capacity than the aluminum one.
d) faster on the aluminum tray, as it has a lower specific heat than the plastic one.
e) with the same speed on both trays, as they will have the same temperature variation.
Correct answer: a) faster on the aluminum tray, as it has a higher thermal conductivity than the plastic one.
Ice melts faster in the tray which transfers heat at a higher rate ie faster. As metals have greater thermal conductivity, the aluminum tray transfers more heat to the ice and it will melt faster.
Exercise 11
(Enem 2021) In the city of São Paulo, the heat islands are responsible for changing the direction of the flow of the sea breeze that should reach the spring region. But when crossing the heat island, the sea breeze now encounters a vertical airflow, which transfers for her the thermal energy absorbed from the hot surfaces of the city, displacing it to high places altitudes. In this way, there is condensation and heavy rain in the center of the city, instead of in the spring region. The image shows the three subsystems that exchange energy in this phenomenon.
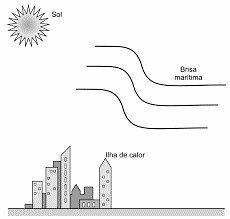
These mechanisms are, respectively,
a) irradiation and convection.
b) irradiation and irradiation.
c) conduction and irradiation.
d) convection and irradiation.
e) convection and convection.
Correct answer: a) irradiation and convection.
Irradiation is the process of transferring heat between the sun and cities. In this process, heat is transferred by electromagnetic radiation.
Convection is the process of transferring heat between heat islands and the sea breeze. In this process, heat is transferred by a fluid medium, in this case, air, through its movements. In convection, the hot air that expands, becomes less dense and rises. The cooler air at higher altitudes, denser, descends creating air currents that exchange heat.
Exercises on Latent Heat and Sensitive Heat
Exercise 12
(Enem 2015) The high combustion temperatures and friction between its moving parts are some of the factors that cause internal combustion engines to heat up. To prevent overheating and consequent damage to these engines, current cooling systems were developed, in which a fluid cooler with special properties circulates through the interior of the engine, absorbing the heat that, when passing through the radiator, is transferred to the atmosphere.
What property must the coolant have to fulfill its purpose most efficiently?
a) High specific heat.
b) High latent heat of fusion.
c) Low thermal conductivity.
d) Low boiling temperature.
e) High coefficient of thermal expansion.
Correct answer: a) High specific heat.
Specific heat is a property of the material, in this case, the coolant. It indicates the amount of heat it needs to receive or give away for one unit of mass, to vary one unit of temperature.
In other words, the higher the specific heat, the more heat it can receive without increasing its temperature too much. Substances with high specific heat have less sensitivity to temperature change.
In this way, coolant with high specific heat can "collect" a greater amount of thermal energy from the engine without boiling.
Exercise 13
(FATEC 2014) In a class in the discipline of Physics in the Welding course at Fatec, the responsible teacher takes up with the students a topic they had seen in high school. Explains how to perform the analysis of a change of state graph of a given hypothetical pure substance. For this, we just need to evaluate the physical quantities represented on the axes and the graph formed by the relationship between these quantities. In this graph, the section that presents an inclination indicates a change in temperature due to energy absorption, and the one that presents a plateau (horizontal section) indicates a change in state due to energy absorption.
After this explanation, he asks the students what was the total amount of energy absorbed by the substance between the end of the change of state for the liquid, until the end of the change of state for the gaseous.

The correct answer to this question, in calories, is
a) 2000.
b) 4000.
c) 6,000.
d) 10 000.
e) 14 000.
Correct answer: d) 10 000.
This change takes place between 4000 and 14000 calories. The substance is fully in a liquid state when the ramp starts after the first plateau. The transformation from liquid to gaseous phase takes place on the second plateau.
Exercises on Thermal Dilation
Exercise 14
(URCA 2012) The radius of the base of a metallic cone, whose density is equal to 10 g/cm3, has at 0°C an initial length Ro = 2 cm. By heating this cone up to a temperature of 100°C, its height varies Δh = 0.015 cm. With a cone mass of 100 g, the mean linear expansion coefficient of the material is:
Right answer:
Objective: determine the coefficient of linear expansion ().
Data = 0.015 cm
Initial radius, = 2 cm = 100°C
mass, m = 100 g
density, d = 10 g/cm3
Mathematical and physical model of linear thermal expansion
Where, is the coefficient of linear expansion.
is the height variation.
is the starting height.
is the variation in temperature.
Isolating ,
and
They are provided. In this way, to determine
, it is necessary to determine
.
To determine let's use the volume and density ratios.
cone volume
Density
Isolating V,
Substituting the value of V and r in the volume equation and making = 3,
Now we can replace in the equation of the coefficient of thermal expansion,
turning into scientific notation
0,0006 =
learn more about
- heat and temperature.
- heat propagation
- sensitive heat
- Specific heat
- Thermal energy
- Thermal expansion
- Thermal Capacity
- thermal conduction
- Thermal Convection
- Thermal Irradiation