Traction, or voltage, is the name given to the strength which is exerted on a body by means of ropes, cables or wires, for example. The pulling force is particularly useful when you want a force to be transferred to other distant bodies or to change the direction of application of a force.
Lookalso: Know what to study in Mechanics for the Enem test
How to calculate the pulling force?
To calculate the pulling force, we must apply our knowledge of the three laws of Newton, therefore, we encourage you to review the fundamentals of Dynamics by accessing our article on at Newton's Laws (just access the link) before proceeding with the study in this text.
O traction calculation takes into account how it is applied, and this depends on multiple factors, such as the number of bodies that make up the system. be studied, the angle that is formed between the pulling force and the horizontal direction and also the state of motion of the bodies.

The rope attached to the cars above is used to transfer a force, which pulls one of the cars.
So that we can explain how traction is calculated, we are going to do it based on different situations, often required in Physics exams for university entrance exams and in the And either.
Traction applied on a body
The first case is the simplest of all: it is when some body, like the block represented in the following figure, is pulledperanrope. To illustrate this situation, we choose a body of mass m that rests on a frictionless surface. In the following case, as in the other cases, the normal force and the body weight force were purposely omitted, in order to facilitate the visualization of each case. Watch:

When the only force applied to a body is an external pull, as shown in the figure above, this pull will be equal to strengthresultant about the body. According to the Newton's 2nd Law, this net force will be equal to the productof its mass by acceleration, thus, the pull can be calculated as:

T – Traction (N)
m – mass (kg)
The – acceleration (m/s²)
Traction applied to a body supported on a friction surface
When we apply a traction force on a body that is supported on a rough surface, this surface produces a frictional force contrary to the direction of the pulling force. According to the behavior of the friction force, while the traction remains lower than the maximum strengthinfrictionstatic, the body remains in balance (a = 0). Now, when the traction exerted exceeds this mark, the friction force will become a strengthinfrictiondynamic.

Funtil - Frictional force
In the case above, the pulling force can be calculated from the net force on the block. Watch:

Traction between bodies of the same system
When two or more bodies in a system are wired together, they move together with the same acceleration. In order to determine the traction force that one body exerts on the other, we calculate the net force in each of the bodies.

Ta, b – Traction that body A does on body B.
Tb, the – Traction that body B does on body A.
In the case above, it is possible to see that only one cable connects bodies A and B, moreover, we see that body B pulls body A through traction Tb, a. According to Newton's third law, the law of action and reaction, the force that body A exerts on the body B is equal to the force that body B exerts on body A, however, these forces have meanings opposites.

Traction between suspended block and supported block
In the case where a suspended body pulls another body through a cable that passes through a pulley, we can calculate the tension on the wire or the tension acting on each of the blocks through the second law of Newton. In this case, when there is no friction between the supported block and the surface, the net force on the body system is the weight of the suspended body (FORB). Note the following figure, which shows an example of this type of system:

In the case above, we must calculate the net force in each of the blocks. By doing this, we find the following result:
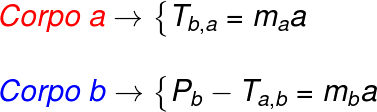
See too: Learn to solve exercises on Newton's laws
Inclined traction
When a body that is placed on a smooth and frictionless inclined plane is pulled by a cable or rope, the pulling force on that body can be calculated in accordance with the componenthorizontal (FORX) of the body weight. Note this case in the following figure:
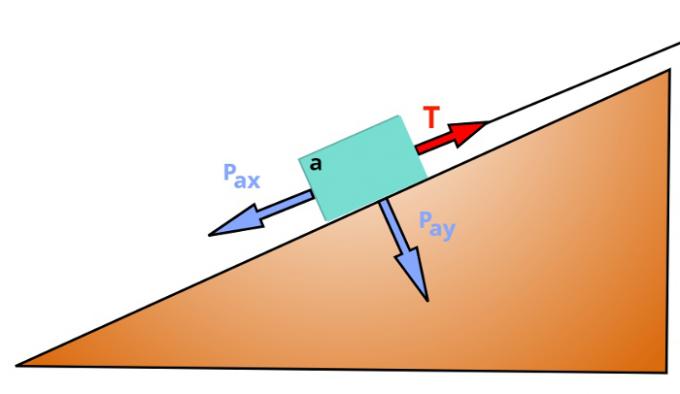
FORAX – horizontal component of the weight of block A
FORYY – vertical component of the weight of block A
The traction applied on block A can be calculated using the following expression:
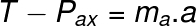
Traction between a body suspended by cable and a body on an inclined plane
In some exercises, it is common to use a system in which the body that is supported on the incline is pulledperabodysuspended, through a rope that passes through a pulley.

In the figure above, we have drawn the two components of the weight force of block A, FORAX and FORYY. The force responsible for moving this system of bodies is the resultant between the weight of block B, suspended, and the horizontal component of the weight of block A:

pendulum pull
In the case of the movement of pendulums, which move according to a trajectoryCircular, the pulling force produced by the yarn acts as one of the components of the centripetal force. At the lowest point of the trajectory, for example, the resulting force is given by the difference between traction and weight. Note a schematic of this type of system:

At the lowest point of pendulum motion, the difference between traction and weight produces centripetal force.
As said, the centripetal force is the resultant force between the traction force and the weight force, thus, we will have the following system:

FCP – centripetal force (N)
Based on the examples shown above, you can get a general idea of how to solve exercises that require the calculation of the pulling force. As with any other type of force, the pulling force must be calculated by applying our knowledge of Newton's three laws. In the following topic, we present some examples of solved exercises about traction force so that you can better understand it.
Solved exercises on traction
Question 1 - (IFCE) In the figure below, the inextensible wire that joins bodies A and B and the pulley have negligible masses. The bodies' masses are mA = 4.0 kg and mB = 6.0 kg. Disregarding the friction between body A and the surface, the acceleration of the set, in m/s2, is (consider the acceleration of gravity 10.0 m/sec2)?
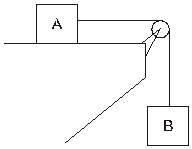
a) 4.0
b) 6.0
c) 8.0
d) 10.0
e) 12.0
Feedback: Letter B
Resolution:
In order to solve the exercise, it is necessary to apply Newton's second law to the system as a whole. By doing this, we see that the weight force is the resultant that makes the whole system move, thus, we must solve the following calculation:

Question 2 - (UFRGS) Two blocks, of mass m1=3.0 kg and m2=1.0 kg, connected by an inextensible wire, can slide without friction on a horizontal plane. These blocks are pulled by a horizontal force F of modulus F = 6 N, as shown in the following figure (disregard the mass of the wire).
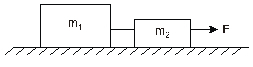
The tension in the wire connecting the two blocks is
a) zero
b) 2.0 N
c) 3.0 N
d) 4.5 N
e) 6.0 N
Feedback: Letter D
Resolution:
To solve the exercise, just realize that the only force that moves the mass block m1 it is the pulling force that the wire makes on it, so it is the net force. So, to solve this exercise, we find the acceleration of the system and then do the traction calculation:
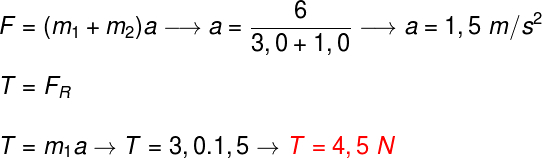
Question 3 - (EsPCEx) An elevator has a mass of 1500 kg. Considering the acceleration of gravity equal to 10 m/s², the traction on the elevator cable, when it ascends empty, with an acceleration of 3 m/s², is:
a) 4500 N
b) 6000 N
c) 15500 N
d) 17,000 N
e) 19500 N
Feedback: Letter e
Resolution:
To calculate the intensity of the traction force exerted by the cable on the elevator, we apply the second law of Newton, in this way, we find that the difference between traction and weight is equivalent to the net force, hence we concluded that:

Question 4 - (CTFMG) The following figure illustrates an Atwood machine.
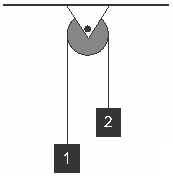
Assuming that this machine has a pulley and a cable with negligible masses and that friction is also negligible, the modulus of acceleration of blocks with masses equal to m1 = 1.0 kg and m2 = 3.0 kg, in m/s², is:
a) 20
b) 10
c) 5
d) 2
Feedback: Letter C
Resolution:
To calculate the acceleration of this system, it is necessary to note that the net force is determined by the difference between the weights of bodies 1 and 2, doing this, just apply the second Newton's law:

By Me. Rafael Helerbrock
