In thermodynamic studies, we saw that thermal expansion is nothing more than the increase in the dimensions of a body when there is an increase in temperature. We can say that this occurs with almost all materials in solid, liquid or gaseous state. Based on linear dilation, where we can calculate the increase in size of a body in a single dimension, we'll see how to calculate the surface dilation, that is, the increase in its surface area when the body is heated.
Surface dilation of solids
Let's consider a sheet metal (figure above) whose dimensions, at temperature T0, are: width L0 and height L0. Therefore, your area is: A0 = L02. Now, if we heat this plate to a temperature T, greater than the initial temperature, we'll see that the plate will expand, having a larger area (A) than the initial area, as shown in the figure below.
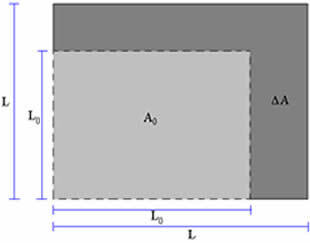
According to the figure above, we see that the metallic plate, after being heated, had its dimensions increased, that is, there was an increase in its area. In order to calculate the increase in area (ΔA = A – A
0), when the sheet metal is subjected to a temperature variation (ΔT = T – T0), we use an equation similar to the equation that provides linear expansion, so we have:ΔA=A0 .β .ΔT or A=A0 (1+ β. ΔT)
Where THE0 is the initial area of the plate, β is the coefficient of surface expansion of the sheet and ΔT is the temperature variation of the sheet metal. We have to remember that β = 2.α. In SI the units are m², K-1 and K. It is important to remember that, although Kelvin is the adopted SI unit, the °C is more common-1 and the °C.
By Domitiano Marques
Graduated in Physics
Source: Brazil School - https://brasilescola.uol.com.br/fisica/dilatacao-superficial-dos-solidos.htm