THE geometryflat is the field of study that focuses on objects belonging to the flat, that is, all its elements (point, line and polygons) are “in” the plane. Geometry had its beginnings in Ancient Greece and is also known as geometryEuclideanflat, in honor of a great scholar in the field named Euclid. Alexandrian mathematician Euclid is known as the "father of geometry".
Read too: Spatial geometry - study of figures with three dimensions
plane geometry concepts
Some concepts are essential to understand plane geometry, but they are not demonstrable, being called primitive concepts. Are they:
Point
The point has no dimension and let's represent it by a capital letter.

straight
The line has one dimension, the length, and is represented by a lowercase letter. The line is infinite.
From the concept of straight line, we can define three other concepts: straight line segment, semi-straight line and angle.
– straight segment
The line segment is defined by a line delimited by two distinct points, that is, a line with a beginning and an end.
– semi-rectal
A ray is defined as a straight line with a beginning and no end, that is, it will be infinite in one of the directions.

– Angle
O angle is used to measure the space between two straight, ray, or straight line segments. When we measure an angle, we are determining its amplitude.

Flat
The plane has two dimensions and is represented by a Greek letter (α, β, γ, … ).

See too: Point, Line, Plane and Space: Basics of Plane Geometry
Formulas and main figures of plane geometry
Now we'll look at the main formulas for calculating areas of flat figures.
triangle
To calculate the area of a triangle, just multiply the base measure (b) with the height measure (h) and divide the result by two.


Square
We know the sides of the square are all the same. To calculate its area, we multiply the base measure with the height measure. Since the measurements are the same, multiplying them is the same as squaring the side.
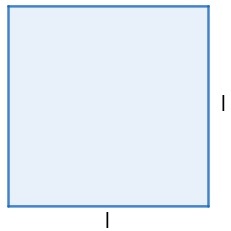

Rectangle
The area of rectangle is given by multiplying the base by the height.
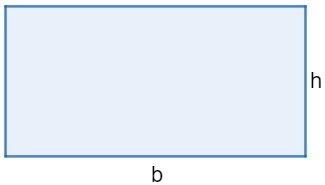

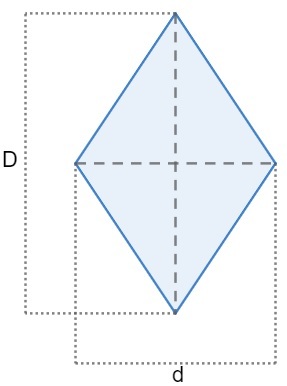
Diamond
The area of diamond is given by the product of the major diagonal (D) and the minor diagonal (d) divided by two.

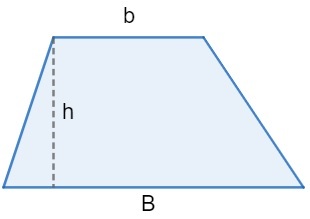
trapeze
The area of trapeze is given by the product of the height and the sum of the major base (B) and the minor base (b) divided by two.

Circle
The area of circle of radius r is given by the product of the radius squared with the irrational number ℼ (usually we use the value ℼ = 3.14).


See too: Geometric solids area - formulas and examples
plane and spatial geometry
THE plane geometry it is characterized by having all its elements contained in the plane. Thus, no object in plane geometry has volume, but area. But the real world doesn't just have two dimensions, right? You, right now, can move back and forth (one dimension), to the right and to the left (one more dimension) and, finally, rotate into an office chair (one more dimension), ie three dimensions.
THE spatial geometry it is about studying objects that are in the third dimension. Some of the structures studied in spatial geometry are present in our daily lives, such as spheres, cones, cylinders and cobblestones.
Plane Geometry in Enem
Plane geometry has many applications in our daily lives. Due to its wide applicability, there is a range of problems that can be explored and, consequently, this subject appears frequently in questions regarding entrance exams and Enem.
Plane geometry questions demand constructive and logical reasoning from the student. The great difficulty of the questions is not with the geometric concepts themselves, but with the involvement of themes such as first degree equation, second degree equation, operations with fractions, percentage and proportion. Let's look at some examples.
→ Example 1
(Enem/2012) On February 20, 2011, the Bulusan volcano erupted in the Philippines. Its geographic location on the globe is given by GPS with a longitude of 124° 3’ 0’’ east of the Greenwich Meridian. (Given: 1st equals 60’ and 1 equals 60″.)
PAVARIN, G. Galileo, Feb. 2012 (adapted)
The angular representation of the volcano's location with respect to its longitude in decimal form is:
a) 124.02°
b) 124.05°
c) 124.20°
d) 124.30°
e) 124.50°
Solution
To solve the exercise, we must transform 124° 3’ and 0″ (read: one hundred and twenty-four degrees, three minutes and zero seconds) to degrees. For this, we just write the 3 minutes in degrees and, since the location has 0″, there is nothing to be done.
It was provided by the exercise that 1° is equivalent to 60’. Let's use a simple rule of three to determine how many degrees we have in 3 minutes.
1° – – – 60’
xx – – – 3’
60x = 3
x = 3 ÷ 60
x = 0.05°
Thus, 124° 3’ and 0″ is equivalent to writing:
124° + 0,05° + 0°
124,05°
Response: alternative b.
→Example 2
(Enem/2011) A school has an empty terrain in a rectangular shape whose perimeter is 40 m, where the intention is to carry out a single construction that takes advantage of as much area as possible. After an analysis carried out by an engineer, he concluded that, to reach the maximum area of the land with a single construction, the ideal work would be:
a) an 8 m bathroom2.
b) a 16 m classroom2.
c) an auditorium with 36 m2.
d) a yard with 100 m2.
e) a block with 160 m2.
Solution
Since we don't know the dimensions of the rectangular terrain, let's name them x and y.

According to the statement, the perimeter is equal to 40 m, that is, the sum of all sides is equal to 40 m, therefore:
x + x + y + y = 40
2x + 2y = 40
2(x +y) = 40
x + y = 20
y = 20 - x
We also know that the area of a rectangle is given by the product of the base and the height, like this:
A = x · y
Substituting the value of y, isolated earlier, we have:
A = x · (20 - x)
A = - x2 + 20x
Now, to know what the maximum area is, just determine the value function maximum A, that is, determine the vertex of the parabola. the value of xv It is given by:

To determine the y valuev, let's replace the value of xv in function A.
A = - x2 + 20x
A = – (10)2 + 20(10)
A = – 100 + 200
A = 100 m2
Therefore, the maximum area is 100 m2.
Response: alternative d.

solved exercises
question 1 – Knowing that the area of the trapeze below is 18 m2, determine the value of x.

Resolution
As the area is equal to 18 m2, we can substitute it in the formula of the trapezium area, as well as the values of the measures given by the problem. Look:

Solving now the equation of the second degree, we have:

Note that the value of x in the problem depicts a measure of length, so it can only assume a positive value, so:
x = 3
question 2 – Calculate the area of the diamond that has the largest diagonal as twice the smallest.
Resolution
Since we don't know the values of the diagonals, let's name them by x.
Minor diagonal (d) → x
Larger diagonal (D) → 2x
And replacing this information in the formula, we have:

by Robson Luiz
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/geometria-plana.htm