When comparing geometric figures, there are some possible conclusions: The figures are congruent, that is, their sides and angles have the same measurements; the figures are different or the figures are similar, that is, they have corresponding angles with equal measures and corresponding sides with proportional measures.
A mathematician named Thales of Miletus observed that there is proportionality between the straight lines formed by a bundle of parallel lines cut by transversal lines. Look at the following image:
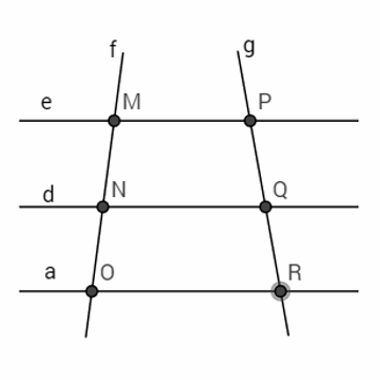
The valid proportionality observed by Tales is that of equalities:
MN = BECAUSE = AT THE
MO PR QR
This important discovery was soon observed in triangles. When a triangle ABC is intersected on two of its sides, AB and AC, by a line r and this line is parallel to the remaining side, BC, of the triangle, then these same proportionalities apply., since the vertex A of this triangle can be seen as a point belonging to a line also parallel to r. Watch:

In this triangle, the following proportionalities apply:
AE = AF = EB
AB AC FC
Once these proportionalities are observed, and considering the triangles AEF and ABC as distinct triangles, it is enough to observe that the angle internal vertex A is common to the two triangles to assert that they are similar, by the case of similarity Side – angle – side (LAL). More specifically:
The internal angle of vertex A is common to the two triangles, so it is the same when comparing the two.
Sides AE and AF belonging to triangle AEF are proportional to sides AC and AB belonging to triangle ABC.
Therefore, by the LAL case of triangle similarity, the triangles are similar.
In summary, having any triangle as a base, you can arrive at the following property: In a triangle ABC, a line r intersects sides AB and AC at points E and F so that line r is parallel to side BC. So triangles ABC and AEF are similar.

This property became known as the fundamental similarity theorem.
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/teorema-fundamental-semelhanca.htm

