Fractional algebraic expressions are those in which the denominator has letters, that is, variable terms. See the examples:
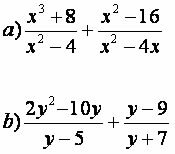
In the case of these algebraic fractions, before performing the sum, we must apply the calculation of mmc, in the in order to match the denominators, as we know that we only add fractions with denominators equals.
To determine the mmc of polynomials, we factor each polynomial individually, and then multiply all factors without repeating the commons. The use of factoring cases is extremely important to determine some situations involving mmc. Note the calculation of mmc between polynomials in the following examples:
Example 1
mmc between 10x and 5x² – 15x
10x = 2 * 5 * x
5x² - 15x = 5x * (x - 3)
mmc = 2 * 5 * x * (x – 3) = 10x * (x – 3) or 10x² – 30x
Example 2
mmc between 6x and 2x³ + 10x²
6x = 2 * 3 * x
2x³ + 10x² = 2x² * (x + 5)
mmc = 2 * 3 * x² * (x + 5) = 6x² * (x + 5) or 6x³ + 30x²
Example 3
mmc between x² - 3x + xy - 3y and x² - y²
x² - 3x+ xy - 3y = x (x – 3)+ y (x – 3) = (x + y) * (x – 3)
x² - y² = (x + y) * (x - y)
mmc = (x – 3) * (x + y) * (x – y)
Example 4
mmc between x³ + 8 and the trinomial x² + 4x + 4.
x³ + 8 = (x + 2) * (x² – 2x + 4).
x² + 4x + 4 = (x + 2)²
mmc = (x + 2)² * (x² - 2x + 4)
by Mark Noah
Graduated in Mathematics
Brazil School Team
Polynomial - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/minimo-multiplo-comum-polinomios.htm
