Lens Manufacturers Equation

The lens manufacturer equation is a mathematical formula that relates to vergence, the focal length, refractive indices of the lens and the medium in which the lens is located, as well as the radii of curvature of the inner and outer sides of the lens. Through this equation, it is possible to manufacture lenses with different grades, for different purposes.

See too:Optics - part of Physics that studies phenomena related to light

Lenses and Lenses Study

O studyof thelenses allows you to understand how the material and shape in which a lens is made affect its ability to change the direction of propagation of the lenses. light rays that cross it. Lenses are homogeneous and transparent optical media that promote the light refraction. When a beam of light passes through a lensconvergent, the light rays that compose it come closer. when we have a lensdivergent, the light rays move away. If you are not very familiar with these concepts, we suggest that you read the following text for a base: Main concepts of geometric optics.

spherical lenses

There are flat lenses and also spherical lenses. The latter are widely used for the correction ofproblemsvisuals, being employed in glasses is on lensesincontact. Among spherical lenses, we emphasize the importance of two types of lens: the concave lenses and at convex lenses.

There are two categories of spherical lenses and six types of lenses in total.

Lens Manufacturers Equation

As noted, the shape of spherical lenses affects the way they direct light beams. Exactly how the lens geometry does this is described by the Halley's equation, also known as the lens manufacturers equation, since it is through it that the lenses used in the correction of visual problems are built.

The lens maker's equation is used to calculate the degree, or vergence, of a spherical lens. The lens grade, in this case, is called diopter, and its unit of measure is the m^-¹ or simply di. So when we refer to a +2 degree lens, that lens has a +2 di vergence.

The sign that appears in front of the diopter indicates if the lens is convergent, in case positive sign, or divergent, when the sign is negative. Converging lenses cause light rays to cross at a point closer to the lens, while lenses divergents distance the point at which the light rays cross, so they are used to correct different problems of the human vision.

THE lens manufacturers equation is as follows:

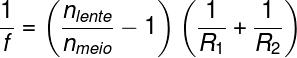
f – lens focal length

no_lens and not_quite – refractive indices of lens and medium

R₁ and R₂– rays of lens faces

You radius of curvature R₁ and R₂ it is the radii of the spherical caps that give rise to spherical lenses.

It is important to emphasize that the radius of curvature of the plane faces (if any) is infinite. In this case, one of the terms(1/R₁ or 1/R₂) becomes equal to zero. Also, n₁ and not₂ they are the refraction indices the lens and the medium in which the lens is immersed, respectively.

See too:Optical Phenomena — Extraordinary Events Resulting from the Interaction of Light with Matter

Solved Exercises on the Lens Manufacturers Equation

Question 1 — Determine the vergence of a hemispherical lens produced from a droplet of glycerin deposited on a small hole with a diameter equal to 5 mm (thus, the radius of this lens is 2.5 mm). Consider the refractive index of glycerin equal to 1.5.

a) + 200 days

b) – 200 days

c) + 400 days

d) – 400 days

Resolution:

Let's use the manufacturers equation of lenses to resolve this issue, but before that, as one of the sides of the glycerin drop is flat, your radius of curvature is infinitely large, and any number divided by an infinitely large number approaches zero, so the lens maker's equation gets a little simpler. Watch:

Based on the calculation, the correct alternative is the letter a.

Question 2 — Determine the focal length of the lens described in the previous question and also the magnification produced by it, if we place an object at a distance of 4 mm from that lens.

a) + 0.025 m and + 2

b) - 0.005 m and + 5

c) + 0.005 m and + 5

d) – 0.04 m and -4

Resolution:

To find the focus, it is necessary to use the vergence result obtained in the previous exercise.

To determine the magnification of this lens, we need to calculate the transverse linear increase.

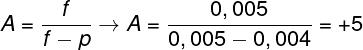
Based on the results, we find that the focus of this lens is equal to 0.005 m and that the linear magnification of this lens, for the specified distance, is equal to +5, so the correct alternative is the letter C.

By Rafael Hellerbrock
Physics teacher 

Source: Brazil School - https://brasilescola.uol.com.br/fisica/equacao-dos-fabricantes-lentes.htm