THE area of a flat figure is the measurement from the surface of the figure. To calculate the area of a flat figure, we use a specific formula that depends on the shape of the figure. The main flat figures are the triangle, circle, square, rectangle, rhombus and trapezoid, and each of them has a formula for calculating the area..
It is noteworthy that the area is studied in plane geometry, the geometry for two-dimensional objects. Geometric objects that have three dimensions are studied in spatial geometry.
Read too: What are the differences between flat and spatial figures?
Summary on flat figures area
The area of a flat figure is the measure of the figure's surface.
-
The main flat figures are:
triangle
Square
Rectangle
Diamond
trapeze
To calculate the area of these plane figures, we use the formulas:

Video lesson on flat figures area
What are the main flat figures?
In order to understand the formula for the area of each plane figure, it is important to be aware of the main plane figures. They are the triangle, square, rectangle, rhombus, trapezoid and circle.
triangle
O triangle is the simplest polygon we know, as it is formed by three sides and three angles:
The triangle is the simplest polygon, as it is the polygon with fewer sides. However, due to its wide application in everyday situations of geometry, it is well studied.
See too: What are the remarkable points of a triangle?
Square
O whatsquare is a quadrilateral, that is, four-sided polygon, which has all right angles and all sides congruent.

the square is a quadrilateral regular that has congruent sides and angles.
Rectangle
we know how rectangle the quadrilateral that has all right angles, that is, the four angles measure 90º.

A square is a particular case of a rectangle because, in addition to the 90º angles, it also has congruent sides. To be a rectangle, just be a quadrilateral that has all the right angles.
Diamond
the diamond is a quadrilateral that has all congruent sides, that is, all sides have the same measurement.

A square is a particular case of a diamond, as it also has all congruent sides. A very important element in the diamond is its diagonal.
trapeze
The trapeze is another particular case of a quadrilateral. To be considered a trapeze, the quadrilateral must have two parallel sides and two non-parallel sidesthereyou.
See too: What are the elements of a polygon?
Circle
O çcircle, unlike all the figures presented above, it is not a polygon, as it does not have sides. the circle is the flat figure formed by all points that are equidistant from the center.
Flat Figure Area Formulas
Each flat figure has a specific formula for calculating its area, let's see what they are.
triangle area
Given a triangle, it is necessary to know the measurement of its base and its height to calculate the area:

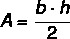
b→base
h → height
Example:
Calculate the area of a triangle that has a base measuring 10 cm and a height equal to 8 cm.
We have to:
b = 10
h = 8
Substituting in the formula, we have to:

Video lesson about the triangle area
square area
In any square, to calculate its area, it is necessary to know the measurement of one of its sides:

A = l²
l → square side
Example:
What is the area of a square that has sides 5 cm long?
A = l²
A = 5²
H = 25 cm²
rectangle area
In a rectangle it is necessary know the length of your base and gives your Height:
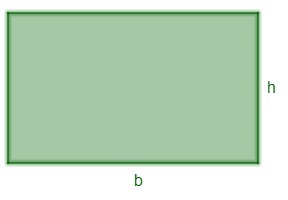
a = b · h
b → base
h → height
Example:
Calculate the area of a rectangle that has sides measuring 6 meters and 4 meters
Regardless of what we define as base or height, the result will be the same, so we will do:
b = 6
h = 4
Thus, the area of the rectangle is:
a = b · h
A = 6 · 4
A = 24 m²
diamond area
Unlike the previous ones, to calculate the area of the diamond, it is necessary to know the measurement of its two diagonals:

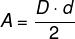
D → major diagonal
d → minor diagonal
Example:
Calculate the area of a diamond that has diagonals measuring 16 cm and 12 cm.
We have to:
D = 16
d = 12
Calculating the area, we have to:

trapeze area
As the trapeze has two bases, a larger and a smaller one, to calculate your area, we need the length of its bases and its height:

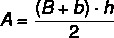
B → Larger base
b → smaller base
h → height
Example:
A trapeze has a larger base measuring 10 cm, a smaller base measuring 6 cm, and a height equal to 8 cm, so its area is:
Data:
B = 10
b = 6
h = 8
Substituting in the formula, we have to:

circle area
In a circle, to calculate your area, we only need the length of the radius, in some cases, we use an approximation for the value of π according to the number of decimal places we want to consider.
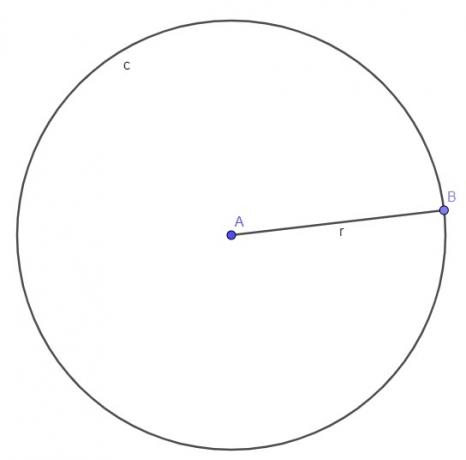
A = πr²
r → radius
Example:
Calculate the area of the circle that has a radius measuring 4 m.
A = πr²
A = π · 4²
A = 16π m²
Read too: Planning of geometric solids - two-dimensional representation of solids
Solved exercises on the area of flat figures
Question 1 - What is the area of a diamond that has the smallest diagonal measuring 5 centimeters, knowing that the largest diagonal is triple the largest diagonal?
A) 35 cm²
B) 37.5 cm²
C) 75 cm²
D) 70 cm²
E) 45 cm²
Resolution
Alternative B
d → shorter diagonal length
D → longest diagonal length
Knowing that the smallest diagonal measures 5 cm and that the largest diagonal measures three times the smallest, then we have to:
d = 5 and D = 5 · 3 = 15
Now calculating the area, we have to:

Question 2 - (IFG 2012) In a rectangle, the ratio between the height measurement and the base measurement is 2/5, and the perimeter of this rectangle measures 42 cm. The area of this rectangle in cm² is equal to:
A) 88
B) 90
C) 91
D) 94
E) 96
Resolution
Alternative B
Let 2x the height and 5x the base, we have to:
P = 2 (2x + 5x) = 42
4x + 10x = 42
14x = 42
x = 42/14
x = 3
So the sides measure:
2x = 2 · 3 = 6
5x = 5 · 3 = 15
Now, just calculate your area:
A = 6 · 15 = 90
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/area-de-figuras-planas.htm


