Compound interest represents the correction applied to an amount that was borrowed or applied. This type of correction is also called interest on interest.
As a content of great applicability, it appears frequently in competitions, entrance exams and on Enem. Therefore, use the questions below to verify your knowledge of this content.
Commented Questions
1) Enem - 2018
A loan agreement provides that when an installment is paid in advance, an interest reduction will be granted in accordance with the advance period. In this case, the present value is paid, which is the value at that time, of an amount that should be paid at a future date. A present value P submitted to compound interest at rate i, for a period of time n, produces a future value V determined by the formula
In a loan agreement with sixty monthly fixed installments, of R$ 820.00, at an interest rate of 1.32% per month, together with the thirtieth installment, another installment will be paid in advance, provided that the discount is greater than 25% of the value of the portion.
Use 0.2877 as an approximation for and 0.0131 as an approximation to ln (1.0132).
The first of the installments that can be anticipated together with the 30th is the
a) 56th
b) 55th
c) 52nd
d) 51st
e) 45th
In the proposed question, we want to find out which installment, applying the interest reduction when paying in advance, the amount paid has a discount greater than 25%, that is:
Simplifying the fraction (dividing top and bottom by 25), discovering that the amount to be paid for the advance installment must be:
The anticipated installment corresponds to the future value corrected to the present value, that is, discounted the 1.32% interest when paying this installment before the term, that is:
Where n is equal to the period to be anticipated. Replacing this expression in the previous one, we have:
As 820 appears on both sides of the inequality, we can simplify, "cutting" this value:
We can invert the fractions, being careful to also invert the sign of inequality. So, our expression is:
Note that the value we want to find is in the exponent (n). Therefore, to solve the inequality we will apply the natural logarithm (ln) on both sides of the inequality, that is:
Now, we can substitute the values indicated in the statement and find the value of n:
As n must be greater than the value found, then we will have to anticipate 22 installments, that is, we will pay the 30th installment together with the 52nd ( 30 + 22 = 52).
Alternative: c) 52nd
2) Enem - 2011
A young investor needs to choose which investment will bring him the greatest financial return in an investment of R$500.00. To do this, it researches the income and tax to be paid on two investments: savings and CDB (bank deposit certificate). The information obtained is summarized in the table:
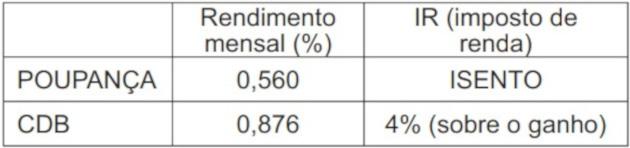
For the young investor, at the end of a month, the most advantageous application is
a) savings, as it will total R$502.80.
b) savings, as it will total an amount of R$ 500.56.
c) the CDB, as it will total an amount of R$504.38.
d) the CDB, as it will total an amount of R$504.21.
e) the CDB, as it will total an amount of R$ 500.87.
To find out what the best yield, let's calculate how much each will yield at the end of a month. So let's start by calculating the savings income.
Considering the problem data, we have:
c = BRL 500.00
i = 0.560% = 0.0056 a.m.
t = 1 month
M = ?
Replacing these values in the compound interest formula, we have:
M = C (1+i)t
Msavings = 500 (1 + 0,0056)1
Msavings = 500.1,0056
Msavings = BRL 502.80
As in this type of application there is no income tax deduction, so this will be the amount redeemed.
Now, let's calculate the values for the CDB. For this application, the interest rate is equal to 0.876% (0.00876). Replacing these values, we have:
MCBD = 500 (1+0,00876)1
MCBD = 500.1,00876
MCBD = BRL 504.38
This amount will not be the amount received by the investor, as in this application there is a 4% discount, relating to income tax, which should be applied on the interest received, as indicated bellow:
J = M - C
J = 504.38 - 500 = 4.38
We need to calculate 4% of this value, just do:
4,38.0,04 = 0,1752
Applying this discount to the value, we find:
504.38 - 0.1752 = BRL 504.21
Alternative: d) the CDB, as it will total an amount of R$504.21.
3) UERJ - 2017
A capital of C reais was invested at compound interest of 10% per month and generated, in three months, an amount of R$53,240. Calculate the value, in reais, of the initial capital C.
We have the following data in the problem:
M = BRL 53240.00
i = 10% = 0.1 per month
t = 3 months
C = ?
Replacing this data in the compound interest formula, we have:
M = C (1+i)t
53240 = C (1+0.1)3
53240 = 1.331 C
4) Fuvest - 2018
Maria wants to buy a TV that is being sold for R$1,500.00 in cash or in 3 monthly interest-free installments of R$500.00. The money that Maria set aside for this purchase is not enough to pay in cash, but she discovered that the bank offers a financial investment that earns 1% a month. After making the calculations, Maria concluded that if she pays the first installment and, on the same day, applies the remaining amount, you will be able to pay the two remaining installments without having to put or take a cent not even. How much did Maria set aside for this purchase, in reais?
a) 1,450.20
b) 1,480.20
c) 1,485.20
d) 1,495.20
e) 1,490.20
In this problem, we have to make the equivalence of values, that is, we know the future value that must be paid in each installment and we want to know the present value (capital that will be applied).
For this situation we use the following formula:
Considering that the application should yield BRL 500.00 at the time of payment of the second installment, which will be 1 month after the payment of the first installment, we have:
To pay the third installment of R$500.00, the amount will be applied for 2 months, so the amount applied will be equal to:
Thus, the amount that Maria set aside for the purchase is equal to the sum of the amounts applied with the amount of the first installment, that is:
V = 500 + 495.05 + 490.15 = BRL 1,485.20
Alternative: c) BRL 1,485.20
5) UNESP - 2005
Mário took a loan of R$8,000.00 at 5% interest per month. Two months later, Mário paid R$5,000.00 of the loan and, one month after this payment, he paid off all his debt. The value of the last payment was:
a) BRL 3,015.
b) BRL 3,820.00.
c) BRL 4,011.00.
d) BRL 5,011.00.
e) BRL 5,250.00.
We know that the loan was paid in two installments and that we have the following data:
VP = 8000
i = 5% = 0.05 a.m
VF1 = 5000
VF2 = x
Considering the data and making the equivalence of capitals, we have:
Alternative: c) R$ 4,011.00.
6) PUC/RJ - 2000
A bank charges an interest rate of 11% per month on its overdraft service. For every 100 reais of overdraft, the bank charges 111 in the first month, 123.21 in the second, and so on. On an amount of 100 reais, at the end of one year the bank will charge approximately:
a) 150 reais.
b) 200 reais
c) 250 reais.
d) 300 reais.
e) 350 reais.
From the information given in the problem, we identified that the correction of the amount charged by the overdraft is by compound interest.
Note that the amount charged for the second month was calculated considering the amount already corrected for the first month, that is:
J = 111. 0.11 = BRL 12.21
M = 111 + 12.21 = BRL 123.21
Therefore, to find the amount that the bank will charge at the end of a year, let's apply the compound interest formula, that is:
M = C (1+i)t
Being:
C = BRL 100.00
i = 11% = 0.11 per month
t = 1 year = 12 months
M = 100 (1+0.11)12
M = 100.1.1112
M = 100,3,498
Alternative: e) 350 reais
To learn more about this topic, read also:
- Percentage
- How to calculate percentage?
- Percentage Exercises
- Math Formulas
- Mathematics in Enem