Chemical Balance Exercises

Chemical balance is one of the subjects that most fall in Enem and entrance exams.

Aspects of reversible reactions are addressed in the questions and the candidates are evaluated both by calculations and by the concepts that involve this theme.

With that in mind, we made this list of questions with different approaches to chemical balance.

Take advantage of the resolution comments to prepare for the exams, and check out the step-by-step instructions on how to solve the questions.

General concepts of chemical equilibrium

1. (Uema) In the equation , after reaching chemical equilibrium, we can conclude the equilibrium constant , about which it is correct to state that:

a) the higher the value of Kc, the lower the yield of the direct reaction.
b) K_ç regardless of temperature.
c) if the speeds of the forward and inverse reactions are equal, then Kc = 0.
d) K_ç it depends on the initial molarities of the reactants.
e) the greater the value of Kc, the greater the concentration of the products.

See Answer

Correct answer: e) the greater the value of Kc, the greater the concentration of the products.

The direct reaction is represented by the number 1, where:

The inverse reaction is represented by

The value of K_ç it is calculated by the ratio between the concentrations of products and reagents.

The numerator (which contains the products) is directly proportional to the equilibrium constant. Therefore, the higher the value of K_ç, the greater the yield of the direct reaction, as more product is being formed and, consequently, the greater the concentration of products.

The value of K_ç varies with temperature, because when we change its value, the endothermic (heat absorption) or exothermic (heat release) reaction can be favored and, with that, more reagent or product can be consumed or created, thus changing the equilibrium constant that depends on the concentration of reagents.

Kc depends on the molar quantities of the components when equilibrium is established and when the rates of the forward and reverse reactions are equal.

2. (UFRN) The chemical balance is characterized by being dynamic at the microscopic level. To obtain quantitative information on the extent of chemical equilibrium, the equilibrium constant quantity is used. Consider the following strip:

Applied to chemical balance, the character's idea of ​​balance:

a) It is correct because, in chemical equilibrium, half the amounts are always products, and the other half are reactants.
b) It is not correct, since, in chemical equilibrium, the concentrations of products and those of reactants can be different, but they are constant.
c) It is correct because, in chemical equilibrium, the concentrations of reactants and products are always the same, as long as the equilibrium is not disturbed by an external effect.
d) It is not correct, since, in chemical equilibrium, the concentrations of the products are always higher than those of the reactants, as long as the equilibrium is not affected by an external factor.
e) It is correct because, in chemical equilibrium, the concentrations of reactants and products are not always the same.

See Answer

Correct answer: b) It is not correct, since, in chemical equilibrium, the concentrations of products and those of reactants can be different, but they are constant.

At equilibrium, the quantities of products and reagents can be calculated based on the constant of balance, and not necessarily should be half the amount of products and the other half reagents.

Equilibrium concentrations are not always the same, they may be different, but constant if no disturbances occur in equilibrium.

Equilibrium concentrations must depend on which reaction is being favored, whether the forward or the reverse. We can know this by the value of K_ç: if K_ç 1, Direct reaction is favored. already if K_ç 1 the reverse reaction is favored.

Chemical Balance Charts

3. (UFPE) At the beginning of the 20th century, the expectation of the First World War generated a great need for nitrogen compounds. Haber pioneered the production of ammonia from nitrogen in the air. If ammonia is placed in a closed container, it decomposes according to the following unbalanced chemical equation: NH_3(g) → N_2(g) + H_2(g). The variations in concentrations over time are illustrated in the following figure:

From the analysis of the figure above, we can state that curves A, B and C represent the temporal variation of the concentrations of the following reaction components, respectively:
a) H₂, no₂ and NH₃
b) NH₃, H₂ and no₂
c) NH₃, no₂ and H₂
d) No₂, H₂ and NH₃
e) H₂, NH₃ and no₂

See Answer

Correct answer: d) N₂, H₂ and NH₃.

1st step: balance the chemical equation.

2 NH_3(g) → N_2(g) + 3 H_2(g)

With the balanced reaction, we realized that it takes 2 moles of ammonia to decompose into nitrogen and hydrogen. Also, the amount of hydrogen produced in the reaction is three times greater than that of ammonia.

2nd step: interpret chart data.

If ammonia is being decomposed, then in the graph its concentration is maximum and decreases, as seen in curve C.

The products, as they are being formed, at the beginning of the reaction the concentrations are zero and increase as the reactant becomes a product.

Since the amount of hydrogen produced is three times greater than that of nitrogen, then the curve for this gas is the largest, as noted in B.

The other product being formed is nitrogen, as seen in curve A.

4. (Cesgranrio) The system represented by the equation was in balance. The equilibrium state was abruptly altered by an addition of substance G. The system reacts to restore balance. Which of the following charts best represents the changes that occurred during the process described?

See Answer

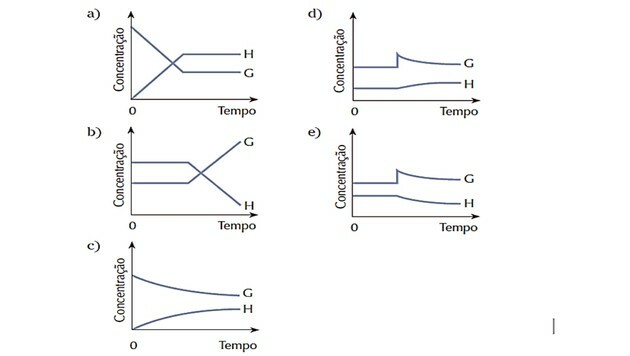
Correct answer: d).

As the system was in equilibrium at the beginning, the amounts of substances G and H remained constant.

The disturbance occurred because the concentration of G increased and the system reacted by transforming this reactant in more product H, shifting the balance to the right, that is, favoring the reaction direct.

We observe that the reagent curve G decreases as it is being consumed, and the product curve H increases as it is being formed.

When a new equilibrium is established, quantities become constant again.

Equilibrium constant: relationship between concentration and pressure

5. (UFRN) Knowing that K_P = K_ç (RT)ⁿ, we can say that K_P = K_ç, for:

steel_2(g) + H_2(g) ↔ CO_(g) + H₂O_(g)
b) H_2(g) + ½ the_2(g) ↔ H₂O₍₁₎
c) No_2(g) + 3 H_2(g) ↔ 2 NH_3(g)
d) NO_(g) + ½ O2_(g) ↔ NO_2(g)
e) 4 FeS_(s) + 7 O_2(g) ↔ 2 Fe₂O_3(s) + 4 SO_2(g)

See Answer

Correct answer: a) CO_2(g) + H_2(g) ↔ CO_(g) + H₂O_(g)

To K_P be equal to K_ç the variation in the number of moles must equal zero, as any number raised to zero results in 1:

K_P = K_ç (RT)⁰
K_P = K_ç x 1
K_P = K_ç

The change in the number of moles is calculated by:

∆n = Number of moles of products - Number of moles of reagents

In this calculation, only the coefficients of substances in the gaseous state participate.

Applying to each alternative equation, we have:

steel2(g) + H2(g) ↔ CO(g) + H2O(g)	∆n = [(1+1) - (1+1)] = 2 - 2 = 0
b) H2(g) + ½ the2(g) ↔ H2O(1)	∆n = [0 - (1+1/2)] = 0 - 3/2 = - 3/2
c) No2(g) + 3 H2(g) ↔ 2 NH3(g)	∆n = [2 - (1+3)] = 2 - 4 = - 2
d) NO(g) + ½ the2(g) ↔ NO2(g)	∆n = [1 - (1+1/2)] = 1 - 3/2 = - 1/2
e) 4 FeS(s) + 7 O2(g) ↔ 2 Fe2O3(s) + 4 SO2(g)	∆n = [(0+4) - (0+7)] = 4 - 7 = - 3

With these results, we can observe that the alternative whose value corresponds to the required result is the one in the first equation.

6. (UEL-adapted) For the reaction represented by the equilibrium constants K_ç and K_P are expressed by the equations: (Given: p = partial pressure)

See Answer

Correct alternative:

The equilibrium constant is calculated by:

Solid compounds, due to their constant concentrations, do not participate in the calculation of K_ç, therefore, the equilibrium constant for the given equation is:

For the equilibrium constant, in terms of pressure, only the gases participate in the calculation, so:

Calculation of the equilibrium constant

7. (Enem/2015) Several acids are used in industries that dispose of their effluents in water bodies, such as rivers and lakes, which can affect the environmental balance. To neutralize the acidity, calcium carbonate salt can be added to the effluent, in appropriate amounts, as it produces bicarbonate, which neutralizes the water. The equations involved in the process are presented:

Based on the values ​​of the equilibrium constants of reactions II, III, and IV at 25°C, what is the numerical value of the equilibrium constant of reaction I?

a) 4.5 x 10^-26
b) 5.0 x 10^-5
c) 0.8 x 10^-9
d) 0.2 x 10⁵
e) 2.2 x 10²⁶

See Answer

Correct answer: b) 5.0 x 10^-5

1st step: use Hess's law to make the necessary adjustments.

Given a chemical equation:

The constant is calculated by:

But if we reverse the equation, we get as a result:

And the constant becomes the inverse:

To arrive at equation 1, given in the question, we need to invert equation II, as in the previous example.

2nd step: Manipulate equations II, III and IV to arrive at the result of equation I.

3rd step: calculate the equilibrium constant of equation I.

Calculating K_I is done by multiplying the constant values.

As in the calculation we have equal powers of bases, we repeat the base and add the exponents.

Since we now have a division with equal powers of bases, we repeat the base and subtract the exponents.

8. (UnB) Phosphorus pentachloride is a very important reagent in organic chemistry. It is prepared in the gas phase through the reaction:
A 3.00 L capacity flask contains at equilibrium, at 200 °C: 0.120 mol PCl_5(g), 0.600 mol of PCl_3(g) and 0.0120 mol of CL_2(g). What is the value of the equilibrium constant at this temperature?

See Answer

Correct answer: 50 (mol/L)^-1

1st step: Assemble the expression of the equilibrium constant for the reaction.

2nd step: calculate the concentrations in mol/L of each component at equilibrium.

Molar Concentration Formula:

PCl3	Cl2	PCl5

3rd step: replace the concentrations in the constant expression and calculate the value of K_ç.

Applications for equilibrium equilibrium

9. (Enem/2016) After their complete wear, the tires can be burned to generate energy. Among the gases generated in the complete combustion of vulcanized rubber, some are pollutants and cause acid rain. To prevent them from escaping into the atmosphere, these gases can be bubbled into an aqueous solution containing a suitable substance. Consider the substance information listed in the table.

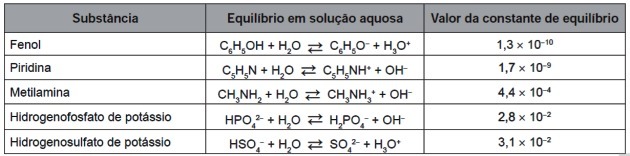
Among the substances listed in the table, the one capable of most efficiently removing polluting gases is (a)

a) Phenol.
b) Pyridine.
c) Methylamine.
d) Potassium hydrogen phosphate.
e) Potassium hydrogen sulfate.

See Answer

Correct answer: d) Potassium hydrogen phosphate.

the CO₂, sulfur oxides (SO₂ and SO₃) and nitrogen oxides (NO and NO₂) are the main polluting gases.

When they react with water present in the atmosphere, there is a acid formation that cause an increase in the acidity of the rain, which is why it is called acid rain.

The equilibrium constants given in the table are calculated by the ratio between the concentrations of products and reagents as follows:

Note that the equilibrium constant is proportional to the concentration of products: the greater the quantity of products, the greater the value of K_ç.

Note the first and last composite values ​​in the table for K_ç:

pyridine
Potassium hydrogen sulfate

Comparing the two numbers, we see that the smaller the negative power, the greater the value of the constant.

To remove pollutants more efficiently, OH^- to react with H ions⁺ present in acids through a neutralization reaction.

Among the substances presented, those that produce the hydroxyls necessary to neutralize acidic compounds are: pyridine, methylamine and potassium hydrogen phosphate.

To find out which compound is the most efficient, we observe the equilibrium constants: the higher the value of the constant, the greater the concentration of OH^-.

Thus, the aqueous solution containing a substance suitable for this purpose is potassium hydrogen phosphate, as it is more basic and neutralizes acids more efficiently.

To learn more, read these texts.:

• ionic balance
• Neutralization reaction

10. (Enem/2009) Soaps are salts of long-chain carboxylic acids used in order to facilitate, during washing processes, the removal of substances of low water solubility, eg oils and fats. The following figure represents the structure of a soap molecule.

In solution, soap anions can hydrolyze water and thereby form the corresponding carboxylic acid. For example, for sodium stearate, the following balance is established:

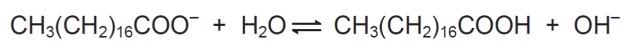
Since the carboxylic acid formed is poorly soluble in water and less efficient in removing fats, the pH of the medium must be controlled in such a way as to prevent the balance above being shifted to the right.

Based on the information in the text, it is correct to conclude that soaps work in a way:

a) More efficient at basic pH.
b) More efficient at acidic pH.
c) More efficient at neutral pH.
d) Efficient over any pH range.
e) More efficient at acidic or neutral pH.

See Answer

Answer: a) More efficient at basic pH.

In the balance shown, we see that sodium stearate when reacting with water forms a carboxylic acid and hydroxyl.

The purpose of controlling the pH is not to allow the formation of carboxylic acid, and this is done by shifting the balance by changing the OH concentration^-.

the more OH^- in solution, there is a disturbance on the products side and the chemical system reacts by consuming the substance that had its concentration increased, in this case the hydroxyl.

Consequently, there will be the transformation of products into reagents.

Therefore, soaps work most efficiently at basic pH as excess hydroxyl shifts the balance to the left.

If the pH were acidic, there would be a higher concentration of H⁺ that would affect the balance by consuming OH^- and the balance would act by producing more hydroxyl, shifting the balance to the left and producing more carboxylic acid, which is not of interest in the presented process.

Chemical equilibrium shift

11. (Enem/2011) Soft drinks have increasingly become the target of public health policies. Glue products contain phosphoric acid, a substance that is harmful to the fixation of calcium, the mineral that is the main component of the teeth matrix. Caries is a dynamic process of imbalance in the process of dental demineralization, loss of minerals due to acidity. It is known that the main component of tooth enamel is a salt called hydroxyapatite. The soda, due to the presence of sucrose, decreases the pH of the biofilm (bacterial plaque), causing the demineralization of the dental enamel. Salivary defense mechanisms take 20 to 30 minutes to normalize the pH level, remineralizing the tooth. The following chemical equation represents this process:

_{GROISMAN, S. Impact of soda on teeth is assessed without taking it off the diet. Available in: http://www.isaude.net. Accessed on: 1 May 2010 (adapted).}

Considering that a person consumes soft drinks daily, a process of dental demineralization may occur, due to the increased concentration of

a) OH^–, which reacts with Ca ions²⁺, shifting balance to the right.
b) H⁺, which reacts with the OH hydroxyls^–, shifting balance to the right.
c) OH^–, which reacts with Ca ions²⁺, shifting balance to the left.
d) H⁺, which reacts with the OH hydroxyls^–, shifting balance to the left.
e) Ca²⁺, which reacts with the OH hydroxyls^–, shifting balance to the left.

See Answer

Correct answer: b) H⁺, which reacts with the OH hydroxyls^–, shifting balance to the right.

When the pH decreases it is because the acidity has increased, that is, the concentration of H ions⁺, as the statement says, there is the presence of phosphoric acid.

These ions react with OH^- causing this substance to be consumed and, consequently, to shift the balance to the right, as the system acts by producing more of these removed ions.

The equilibrium shift between reactants and products occurred due to the decrease in the OH concentration^-.

If the Ca ions²⁺ and oh^- had the concentration increased, it would shift the balance to the left, as the system would react by consuming them and forming more hydroxyapatite.

12. (Enem/2010) Sometimes, when opening a soda, it is noticed that a part of the product quickly leaks from the end of the container. The explanation for this fact is related to the disturbance of the chemical balance existing between some of the product's ingredients according to the equation:

Changing the previous balance, related to refrigerant leakage under the conditions described, results in:

a) CO release₂ for the environment.
b) Raising the temperature of the container.
c) Raising the internal pressure of the vessel.
d) Elevation of CO concentration₂ in the liquid.
e) Formation of a significant amount of H₂O.

See Answer

Correct answer: a) CO release₂ for the environment.

Inside the bottle, the carbon dioxide was dissolved in the liquid due to high pressure.

When the bottle is opened, the pressure inside the container (which was greater) equals the pressure in the environment and, with that, there is an escape of carbon dioxide.

The equilibrium shift between reactants and products occurred due to the decrease in pressure: when the pressure decreases, the equilibrium shifts to the largest volume (number of moles).

The reaction shifted to the left and the CO₂ which was dissolved in the liquid was released, leaking out when the bottle was opened.