Simple and compound interest are calculations performed in order to correct the amounts involved in the transactions financial, that is, the correction made when lending or investing a certain amount during a period of time.
The amount paid or redeemed will depend on the fee charged for the transaction and the period the money will be borrowed or invested. The higher the rate and time, the higher this value.
Difference between simple and compound interest
In simple interest, correction is applied to each period and considers only the initial value. In compound interest, correction is made on already corrected amounts.
For this reason, compound interest is also called interest on interest, that is, the amount is adjusted on an amount that has already been adjusted.
Therefore, for longer periods of investment or loan, correction by compound interest will cause the final amount to be received or paid to be greater than the amount obtained with simple interest.

Most financial operations use the correction by the compound interest system. Simple interest is restricted to short-term operations.
Simple interest formula
Simple interest is calculated using the following formula:
Being,
J: interest
C: initial transaction value, called capital financial mathematics
i: interest rate (amount usually expressed as a percentage)
t: transaction period
We can also calculate the total amount that will be redeemed (in the case of an investment) or the amount to be repaid (in the case of a loan) at the end of a predetermined period.
This value, called the amount, is equal to the sum of the principal plus the interest, that is:
We can substitute the value of J in the formula above and find the following expression for the amount:
The formula we found is an affine function, so the value of the amount grows linearly as a function of time.
Example
If capital of $1000.00 monthly yields $25.00, what is the annual interest rate in the simple interest system?
Solution
First, let's identify each quantity indicated in the problem.
C = BRL 1000.00
J = BRL 25.00
t = 1 month
i = ?
Now that we have identified all the quantities, we can substitute in the interest formula:
However, please note that this fee is monthly as we use the 1 month period. To find the annual fee we need to multiply this value by 12, so we have:
i = 2.5.12 = 30% per year
Compound interest formula
The amount capitalized to compound interest is found by applying the following formula:
Being,
M: amount
C: capital
i: interest rate
t: time period
Unlike simple interest, in this type of capitalization, the formula for calculating the amount involves an exponential variation. Hence it is explained that the final value increases considerably for longer periods.
Example
Calculate the amount produced by R$2,000 applied at the rate of 4% per quarter, after one year, in the compound interest system.
Solution
Identifying the information given, we have:
C = 2000
i = 4% or 0.04 per quarter
t = 1 year = 4 quarters
M = ?
Replacing these values in the compound interest formula, we have:
Therefore, at the end of one year the amount will be equal to R$2,339.71.
Solved Exercises
question 1
Calculation of amount
What is the amount of an investment of R$500.00, at a rate of 3% per month, in a period of 1 year and 6 months, in simple and compound interest systems?
simple interest
Data:
C = 500
i = 0.03
t = 18 months (1 year + 6 months)
The amount will be the starting capital plus interest.
M = C + J
The interest being:
J = C.i.t
J = 500.0.03.18 = 270
So the amount will be:
M = C+J
M = 500+270
M = 770
Answer: The amount of this application will be R$770.00.
Compound interest
Applying the values in the formula, we have:
Answer: The investment amount under the compound interest regime is R$851.21.
question 2
Capital calculation
A certain capital was applied for a period of 6 months. The rate was 5% per month. After this period, the amount was R$5000.00. Determine the capital.
simple interest
Putting C in evidence in the simple interest formula:
M = C + J
M = C + C.i.t
M = C(1+i.t)
Isolating C into the equation:
Compound interest
Isolating C in the compound interest formula and replacing the values:
Answer: The capital must be R$4201.68.
question 3
Interest rate calculation
What would the monthly interest rate be on a $100,000 investment over an eight-month period that earned an amount of $1600.00.
simple interest
Applying the formula and putting C in evidence:
M = C + J
M = C + C.i.t
M = C(1+i.t)
Replacing the values and doing the numerical calculations:
in percentage
I = 7.5%
Compound interest
Let's use the formula for compound interest and divide the amount by the principal.
question 4
Calculation of application period (time)
A capital of R$8000 was invested at a monthly interest of 9%, obtaining an amount of R$10360.00.
How long was this capital invested?
simple interest
Using the formula
Therefore, the time is approximately 3.27 months.
Compound interest
In this step, we are faced with an exponential equation.
To solve it, we will use the logarithm, applying a logarithm of the same base, to both sides of the equation.
Using a property of the logarithms on the right side of the equation, we have:
question 5
UECE - 2018
A store sells a TV set, with the following payment terms: down payment of R$800.00 and a payment of R$450.00 two months later. If the price of the spot TV is R$1,200.00, then the simple monthly interest rate embedded in the payment is
A) 6.25%.
B) 7.05%.
C) 6.40%.
D) 6.90%.
When comparing the price of the TV in cash (R$1,200.00) and the amount paid in two installments, we observe that there was an increase of R$50.00, as the amount paid was equal to R$1,250.00 (800 +450) .
To find the rate charged, we can apply the simple interest formula, considering that the interest was applied on the debit balance (TV value less down payment). So we have:
C = 1200 - 800 = 400
J = 450 - 400 = 50
t = 2 months
J = C.i.t
50 = 400.i.2
Alternative: a) 6.25%
Equivalence of capital
In Financial Mathematics, it is essential to keep in mind that the amounts involved in a transaction will be shifted in time.
Given this fact, making a financial analysis implies comparing present values with future values. Thus, we must have a way to make the equivalence of capital at different times.
When we calculate the amount, in the compound interest formula, we are finding the future value for t time periods, at a rate i, from a present value.
This is done by multiplying the term (1+i)no at present value, that is:
On the contrary, if we want to find the present value knowing the future value, we will do a division, that is:
Example:
To buy a motorcycle at a great price, a person asked for a loan of R$ 6,000.00 from a finance company at 15% monthly interest. Two months later, he paid R$3,000.00 and paid off the debt the following month.
What was the amount of the last installment paid by the person?
Solution
If the person has paid off the amount owed on the loan, then the amount paid in the first installment plus the second installment is equal to the amount owed.
However, the installments were adjusted over the period by monthly interest. Therefore, to match these amounts, we have to know their equivalent values on the same date.
We will carry out the equivalence considering the time of the loan, as shown in the diagram below:
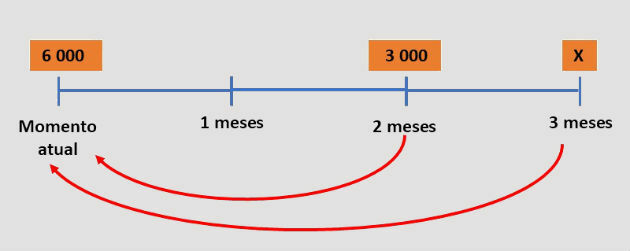
Using the formula for two and three months:
Therefore, the last payment made was R$5,675.25.
Exercise solved
question 6
A loan was made at the monthly rate of i%, using compound interest, in eight fixed installments equal to P.
The debtor has the possibility of repaying the debt in advance at any time, paying for this the current value of the installments still to be paid. After paying the 5th installment, it decides to pay off the debt upon paying the 6th installment.
The expression that corresponds to the total amount paid for the repayment of the loan is:
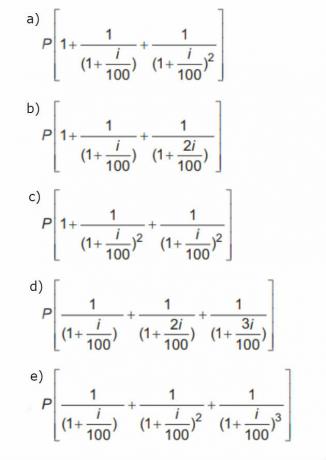
Answer: Letter a



