THE prime factor decomposition is a very important tool in mathematical development, as it is possible to simplify numeric expressions or algebraic and calculate MDC or MMC of whole numbers.
The decomposition into prime factors is one of the most important results within the field of algebra and is formally known as the Fundamental Theorem of Arithmetic, which states that all positive integer greater than 1 can be written (or decomposed) in the form of multiplication of prime numbers.
Read too: Multiplication Properties for Mental Calculation
How to decompose into prime factors?
It is essential to understand the concept of prime numbers, since we are going to use them to break down whole numbers. Here, let's take a brief look at the definition of prime numbers.
|
Prime numbers are those that present in your list of dividers only the number 1 and themselves. To check whether the numbers 11 and 21 are prime or not, for example, we must list the divisors of both numbers: D (11) = {1, 11} D (21) = {1, 3, 7, 21} Note that when listing the divisors of 11, only the number 1 and itself appear, so the number 11 is prime, which does not apply to number 21, which has more numbers than 1 and 21, so the number 21 is not prime. the main Prime numbers that we use to perform the decomposition are the first ones, so it's very important that we know at least the following primes: P = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …} |
Prime factor decomposition is a very powerful tool within mathematics, as it enables the simplification of algebraic and numerical expressions. Formally, the decomposition into prime factors is known as the Fundamental Theorem of Arithmetic, which states:
"Every whole number greater than 1 can be written as a multiplication of prime numbers."
Furthermore, this decomposition is unique for each number, that is, when decomposing the number 12, for example, it will be the only one with such factorization. The number that admits a decomposition is called compound.
How to decompose a composite number?
To decompose a composite number, we must perform divisions successive prime numbers – if division is possible – until the quotient is equal to 1. At the end, we must write the prime numbers used in multiplication form (factored form). See the examples below:
Example 1
Write the number 24 in factored form.
To write the number 24 in factored form, we must divide it by the first prime number that is possible, that is, divide the number 24 by a prime number in which the division is exact.
Using the division algorithm, let's divide the 24 by2.
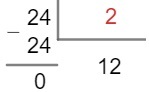
The quotient found now was the number 12, so we must divide it again by the first prime number whose division is exact, that is, by2.
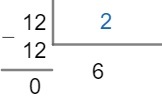
We must continue this process until the quotient is equal to 1. Note that now the quotient is equal to 6, so we can divide it by 2, as the number 2 is the first prime number for which division is still possible.
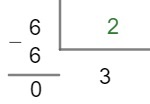
Note that the quotient is now equal to 3, so it is not possible to divide it by 2. In these cases, let's divide it by the next prime number whose division is exact, that is, by3.
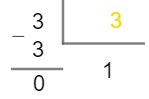
As the quotient is equal to 1, the decomposition has ended, it is now enough to write the prime numbers (which are inside the key) as a product. Look:
24 = 2 · 2 ·2 · 3
24 = 23· 3
See that we've written the number 24 in product form. That means we factored the number 24 using prime numbers.
Example 2
Write the number 25 in its factored form.
In this example, we're going to use the division algorithm again, but we're going to write it differently, see:
25 = 5 · 5 + 0
5 = 5 · 1 + 0
The number 25, in factored form, is:
25 = 5 ·5
25 = 52
Read too: Divisibility criteria - processes that facilitate the division operation
Practical method to perform prime factor decomposition
Looking at the previous method, if the number to be factored is very large, like the number 1024, we have something quite laborious, as successive divisions by prime numbers will be necessary until the quotient is equal to 1.
The method we will see next is nothing more than a simplification of the division. Instead of writing all the elements of the division (divisor, dividend, quotient and remainder), let's put only the prime number by which we're going to divide the number to be factored and the quotient of the division. See the examples:
Factoring the number 60
To factor the number 60, let's follow the same step by step, but let's just write the quotient of the division (that is, the result) and the prime number by which we are going to divide the number 60.

See that when dividing the 60 by2,the result is 30 and by dividing the number 30 by 2, the result is 15, and so on until the result of the division equals 1. The process remains the same, the only difference is in the simplification of information.
The number 60, in its factored form, is:
60 = 2 · 2 · 3 ·5
60 = 22 · 3 · 5

solved exercises
question 1 – Decompose the number 192 into prime factors.
Resolution

The number 192, in its decomposed form, is:
192 = 2 · 2 · 2 · 2 · 2 · 2 · 3
192 = 26 · 3
question 2 – Consider the numbers p and q such that p = 25 · 5 and q = 32. Determine the ratio between q and p.
Resolution
The ratio between two numbers is the division between them. We must always obey the order in which they were given to divide q by p. Before performing the actual division, let's factor the number q, looking for a way to simplify the calculation.

We have q = 32, so we can write it like this:
q = 2 · 2 · 2 · 2 · 2
q = 25
Now since we factored the number q, we can assemble the ratio between q and p and substitute the values.