The angles of 30º, 45º and 60º are called notable because they are the ones we most often calculate.
Therefore, it is important to know the sine, cosine and tangent values of these angles.
Table of notable angles
The table below is very useful and can be easily built by following the steps indicated.
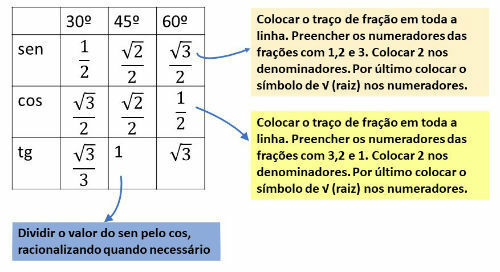
Value of sine and cosine of 30th and 60th
You angles 30º and 60º are complementary, that is, they add up to 90º.
We found the value of 30º sine by calculating the ratio between the opposite side and the hypotenuse. The cosine value of 60º is the ratio between the adjacent side and the hypotenuse.
In this way, the 30º sine and the 60º cosine of the triangle shown below will be given by:

Thus, we find that the value of the sine of 30° is equal to the value of the cosine of 60°. The same happens with the 60th sine and the 30th cosine, because:
So when two angles are complementary, the sine value of one is equal to the cosine value of the other.
To find the value of 30º sine (60º cosine) and 30º cosine (60º sine), let's consider an equilateral triangle ABC with sides equal to L, represented below:
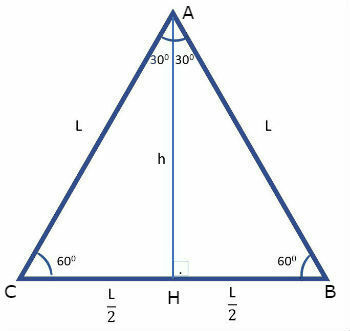
The height (h) of the equilateral triangle coincides with the median, so the height divides the side relative to the middle ().
Also, the height coincides with the bisector. In this way, the angle is also split in half, as shown in the figure.
Let's also consider that the height value is given by:
.
To calculate the sine and cosine of 30º, we will consider the right triangle AHB, which was obtained from the triangle ABC.
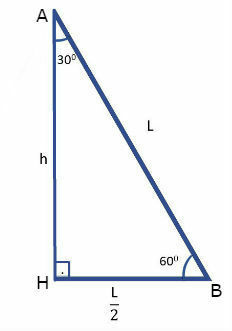
So we have:
and
Value of sine and cosine of 45º
We will calculate the sine and cosine value of the 45° angle, from a square with side L represented below:

The square's diagonal is the bisector of the angle, that is, the diagonal divides the angle in half (45º). Also, the diagonal measures .
To find the sine and cosine value of 45º let's consider the right triangle ABC shown in the figure:
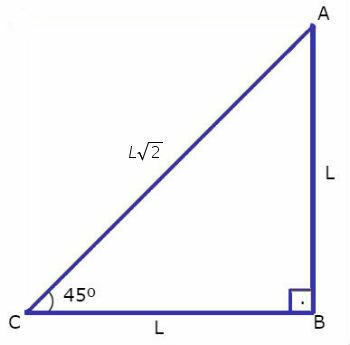
Then:
and
Tangent value of 30th, 45th and 60th
To calculate the tangent of the notable angles we will use the trigonometric ratio:
Thus:
To learn more, read also:
- Trigonometric Table
- Sine, Cosine and Tangent
- Trigonometry in the Rectangle Triangle
- law of sins
- Cosine Law
Solved Exercises
1) A swimmer crosses a river at a 30° angle to one of the banks. Knowing that the width of the river measures 40m, determine the distance traveled by the swimmer to cross the river.
2) Enem - 2010
An atmospheric balloon, launched in Bauru (343 kilometers northwest of São Paulo), last Sunday night, it fell on Monday in Cuiabá Paulista, in the Presidente Prudente region, scaring farmers from region. The artifact is part of the Hibiscus Project program, developed by Brazil, France, Argentina, England and Italy, to measure the behavior of the ozone layer, and its descent took place after compliance with the time
expected measurement.
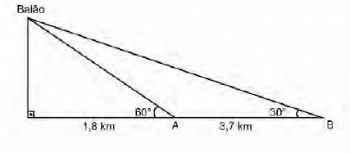
On the date of the event, two people saw the balloon. One was 1.8 km from the balloon's vertical position and saw it at an angle of 60º; the other was 5.5 km from the balloon's vertical position, aligned with the first, and in the same direction, as seen in the figure, and saw it at an angle of 30º.
What is the approximate height of the balloon?
a) 1.8km
b) 1.9km
c) 3.1km
d) 3.7km
e) 5.5km



