Newton's Second Law establishes that the acceleration acquired by a body is directly proportional to the resultant of the forces acting on it.
As acceleration represents the variation in velocity per unit of time, the 2nd Law indicates that forces are the agents that produce variations in velocity in a body.
Also called the fundamental principle of Dynamics, it was conceived by Isaac Newton and forms, together with two other laws (1st Law and Action and Reaction), the foundations of Classical Mechanics.
Formula
We mathematically represent the Second Law as:
Where,
Force and acceleration are vector quantities, so they are represented with an arrow over the letters that indicate them.
As vector quantities, they need, in order to be fully defined, a numerical value, a unit of measure, a direction and a direction. The direction and direction of acceleration will be the same as the net force.
In the 2nd Law, the object's mass (m) is the proportionality constant of the equation and is the measure of the inertia of a body.
In this way, if we apply the same force on two bodies with different masses, the one with the greatest mass will suffer a lower acceleration. Hence, we conclude that the one with greater mass resists more to variations in velocity, therefore, it has greater inertia.

Example:
A body with a mass equal to 15 kg moves with a modulus acceleration equal to 3 m/s2. What is the magnitude of the net force acting on the body?
The force module will be found applying the 2nd law, so we have:
FR = 15. 3 = 45 N
Newton's Three Laws
the physicist and mathematician Isaac Newton (1643-1727) formulated the basic laws of mechanics, where he describes the movements and their causes. The three laws were published in 1687, in the work "Mathematical Principles of Natural Philosophy".
Newton's First Law
Newton was based on the ideas of Galileo on inertia to formulate the 1st Law, therefore, it is also called the Law of Inertia and can be stated:
In the absence of forces, a body at rest remains at rest and a body in motion moves in a straight line with constant velocity.
In short, the Newton's First Law indicates that an object cannot initiate motion, stop or change direction by itself. It takes the action of a force to bring about changes in its state of rest or movement.
Newton's Third Law
THE Newton's Third Law it is the Law of "Action and Reaction". This means that, for every action, there is a reaction of the same intensity, same direction and in the opposite direction. The principle of action and reaction analyzes the interactions that take place between two bodies.
When a body suffers the action of a force, another will receive its reaction. As the action-reaction pair occurs in different bodies, the forces do not balance.
Learn more at:
- Newton's Three Laws
- Gravity
- What is Inertia in Physics?
- Physics Formulas
- Quantity of Movement
- inclined plane
Solved Exercises
1) UFRJ-2006
A block of mass m is lowered and raised using an ideal wire. Initially, the block is lowered with constant vertical acceleration, downward, of module a (by hypothesis, less than the module g of the acceleration of gravity), as shown in figure 1. Then, the block is lifted with constant vertical acceleration, upwards, also of module a, as shown in figure 2. Let T be the yarn tension on the way down and T’ the yarn tension on the way up.
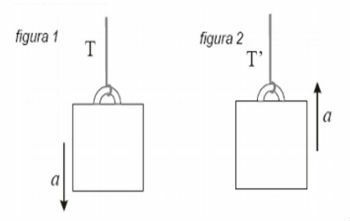
Determine the ratio T’/T as a function of a and g.
In the first situation, as the block is descending, the weight is greater than the traction. So we have that the net force will be: FR=P - T
In the second situation, when going up T' will be greater than the weight, so: FR=T' - P
Applying Newton's 2nd law, and remembering that P = m.g, we have:
Dividing (2) by (1), we find the requested reason:
2) Mackenzie-2005
A 4.0kg body is being lifted by means of a wire that supports maximum traction of 50N. Adopting g = 10m/s2, the greatest vertical acceleration that can be applied to the body, pulling it by this wire, is:
a) 2.5m/s2
b) 2.0m/s2
c) 1.5m/s2
d) 1.0m/s2
e) 0.5m/s2
T - P = m. a (the body is being lifted, so T>P)
As the maximum traction is 50 N and P = m. g = 4. 10 = 40 N, the greatest acceleration will be:
Alternative to: 2.5 m/s2
3) PUC/MG-2007
In the figure, block A has a mass mTHE = 80 kg and block B, a mass mB = 20 kg. Frictions and inertia of the wire and pulley are still negligible and g = 10m/s is considered2 .
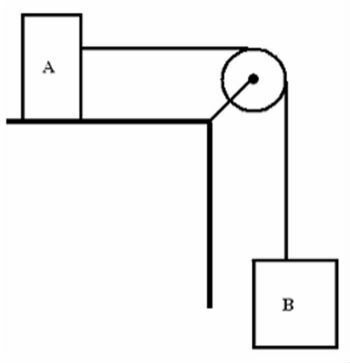
Regarding the acceleration of block B, it can be said that it will be:
a) 10 m/s2 down.
b) 4.0 m/s2 up.
c) 4.0 m/s2 down.
d) 2.0 m/s2 down.
B's weight is the force responsible for moving the blocks down. Considering the blocks as a single system and applying Newton's 2nd Law we have:
PB = (mTHE + mB). The
Alternative d: 2.0 m/s2 down
4) Fatec-2006
Two blocks A and B of masses 10 kg and 20 kg, respectively, joined by a thread of negligible mass, are at rest on a horizontal plane without friction. A force, also horizontal, of intensity F = 60N is applied to block B, as shown in the figure.

The modulus of the traction force in the wire that joins the two blocks, in newtons, is valid
a) 60
b) 50
c) 40
d) 30
e) 20
Considering the two blocks as a single system, we have: F = (mTHE + mB). a, substituting the values we find the acceleration value:
Knowing the value of the acceleration, we can calculate the value of tension in the wire, let's use block A for this:
T=mTHE . The
T = 10. 2 = 20 N
Alternative e: 20 N
5) ITA-1996
Shopping in a supermarket, a student uses two carts. It pushes the first one, of mass m, with a horizontal force F, which, in turn, pushes another one of mass M onto a flat, horizontal floor. If the friction between the carts and the floor can be neglected, it can be said that the force that is applied on the second cart is:
a) F
b) MF / (m + M)
c) F (m + M) / M
d) F / 2
e) another different expression
Considering the two carts as a single system, we have:
To calculate the force acting on the second cart, let's use Newton's 2nd Law for the 2nd cart equation again:
Alternative b: MF/(m+M)