Uniform motion is one whose speed does not change over time. When the motion follows a straight-line trajectory, it is called uniform straight motion (MRU).
Take advantage of the resolved and commented questions below to check your knowledge of this important subject of cinematics.
Entrance Exam Issues Resolved
question 1
(Enem - 2016) Two vehicles that travel with constant speed on a road, in the same direction and direction, must keep a minimum distance from each other. This is because the movement of a vehicle, until it comes to a complete stop, takes place in two stages, from the moment the driver detects a problem that requires a sudden brake. The first step is associated with the distance that the vehicle travels between the time interval between the detection of the problem and the activation of the brakes. The second is related to the distance that the car travels while the brakes act with constant deceleration.
Considering the situation described, which graphic sketch represents the speed of the car in relation to the distance traveled until it comes to a complete stop?
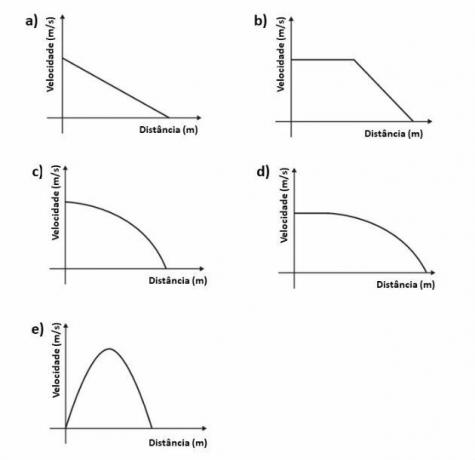
Correct alternative: d
When solving problems with graphs, it is essential to pay close attention to the quantities to which the graph refers.
In the graph of the question, we have the speed as a function of the distance covered. Be careful not to confuse it with the velocity versus time graph!
In the first step indicated in the problem, the speed of the car is constant (MRU). This way, your graph will be a line parallel to the distance axis.
In the second stage, the brakes that give the car a constant deceleration were activated. Therefore, the car has a uniformly varied rectilinear motion (MRUV).
We then need to find an equation that relates velocity to distance in the MRUV.
In this case, we will use the Torricelli equation, indicated below:
v2 = v02 + 2. The. at
Note that in this equation, speed is squared and the car has a deceleration. Therefore, the speed will be given by:
Therefore, the excerpt of the graph relating to the 2nd stage will be a curve with the concavity facing downwards, as shown in the image below:

question 2
(Cefet - MG - 2018) Two friends, Pedro and Francisco, plan to take a bike ride and agree to meet on the way. Pedro is standing at the appointed place, awaiting his friend's arrival. Francisco passes through the meeting point at a constant speed of 9.0 m/s. At the same moment, Pedro starts to move with an also constant acceleration of 0.30 m/s2. The distance traveled by Pedro to reach Francisco, in meters, is equal to
a) 30
b) 60
c) 270
d) 540
Correct alternative: d) 540
Francisco's movement is a uniform movement (constant velocity) and Pedro's is uniformly varied (constant acceleration).
So, we can use the following equations:
When they meet, the distances covered are equal, so let's equalize the two equations, substituting the given values:
Now that we know when the encounter took place, we can calculate the distance covered:
Δs = 9. 60 = 540 m
See too: Kinematics Formulas
question 3
(UFRGS - 2018) In large airports and shopping malls, there are horizontal moving mats to facilitate the movement of people. Consider a belt 48 m long and 1.0 m/s speed. A person enters the treadmill and continues walking on it at a constant speed in the same direction of movement as the treadmill. The person reaches the other end 30 s after entering the treadmill. How fast, in m/s, does the person walk on the treadmill?
a) 2.6
b) 1.6
c) 1.0
d) 0.8
e) 0.6
Correct alternative: e) 0.6
For an observer standing outside the treadmill, the relative speed that he sees the person moving is equal to the speed of the treadmill plus the speed of the person, ie:
vR = vAND + vP
The belt speed is equal to 1 m/s and the relative speed is equal to:
Replacing these values from the previous expression, we have:
See too: Average speed exercises
question 4
(UNESP - 2018) Juliana practices races and manages to run 5.0 km in half an hour. Your next challenge is to participate in the São Silvestre race, which runs 15 km. As it is a longer distance than she is used to running, her instructor instructed her to decrease her usual average speed by 40% during the new test. If you follow the guidance of her instructor, Juliana will complete the São Silvestre race in
a) 2 h 40 min
b) 3:00 am
c) 2 h 15 min
d) 2 h 30 min
e) 1 h 52 min
Correct alternative: d) 2h 30 min
We know that in the São Silvestre race she will decrease her usual average speed by 40%. So, the first calculation will be to find that speed.
For this, let's use the formula:
Since 40% of 10 is equal to 4, we have that its speed will be:
v = 10 - 4 = 6 km/h
question 5
(Unicamp - 2018) Located on the Peruvian coast, Chankillo, the oldest observatory in the Americas, is made up of thirteen towers that line up from north to south along a hill. On December 21, when the summer solstice occurs in the Southern Hemisphere, the Sun rises to the right of the first tower (south), on the far right, from a defined vantage point. As the days pass, the position at which the Sun rises shifts between the towers towards the left (north). You can calculate the day of the year by observing which tower coincides with the sun's position at dawn. On June 21, the winter solstice in the Southern Hemisphere, the Sun rises to the left of the last tower at the far end. left and, as the days go by, it moves towards the right, to restart the cycle in December Following. Knowing that the Chankillo towers are positioned over 300 meters on the north-south axis, the average scalar speed with which the sunrise position moves through the towers is about
a) 0.8 m/day.
b) 1.6 m/day.
c) 25 m/day.
d) 50 m/day.
Correct alternative: b) 1.6 m/day.
The distance between the first tower and the last tower is equal to 300 meters and the Sun takes six months to complete this journey.
Therefore, in one year (365 days) the distance will be equal to 600 meters. Thus, the average scalar velocity will be found by doing:
question 6
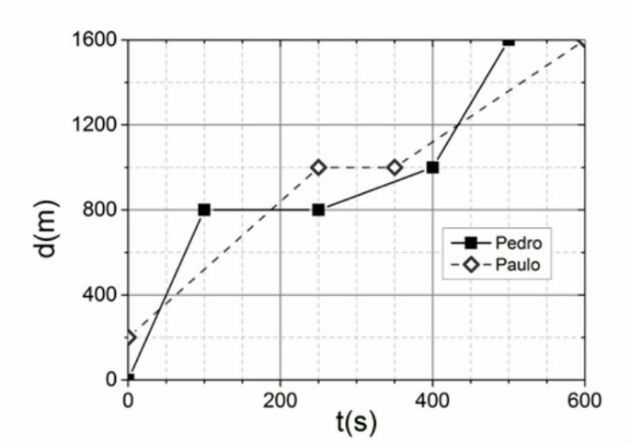
(UFRGS - 2016) Pedro and Paulo daily use bicycles to go to school. The chart below shows how they both covered the distance to school, as a function of time, on a given day.
Based on the chart, consider the following statements.
I - The average speed developed by Pedro was higher than that developed by Paulo.
II - The maximum speed was developed by Paulo.
III- Both were stopped for the same period of time during their journeys.
Which ones are correct?
a) Only I.
b) Only II.
c) Only III.
d) Only II and III.
e) I, II and III.
Correct alternative: a) Only I.
To answer the question, let's look at each statement separately:
I: Let's calculate the average speed of Pedro and Paulo to define which one was higher.
For this, we will use the information shown in the chart.
So Peter's average speed was higher, so this statement is true.
II: To identify the maximum speed, we must analyze the slope of the graph, that is, the angle with respect to the x axis.

Looking at the chart above, we notice that the highest slope corresponds to Peter (red angle) and not Paul, as indicated in statement II.
In this way, statement II is false.
III: The period of stopped time corresponds, in the graph, to the intervals where the straight line is horizontal.
Analyzing the graph, we can see that the time that Paulo was stopped was equal to 100 s, while Pedro was stopped for 150 s.
Therefore, this statement is also false. Therefore, only statement I is true.
question 7
(UERJ - 2010) A rocket chases a plane, both with constant speeds and the same direction. While the rocket travels 4.0 km, the plane travels just 1.0 km. Admit that in an instant t1, the distance between them is 4.0 km and that, at time t2, the rocket reaches the plane.
In time t2 - t1, the distance traveled by the rocket, in kilometers, corresponds approximately to:
a) 4.7
b) 5.3
c) 6.2
d) 8.6
Correct alternative: b) 5.3
With the information from the problem, we can write the equations for the position of the rocket and the plane. Note that at instant t1 (initial moment) the plane is at the 4 km position.
So we can write the following equations:
At the time of the meeting, the positions sF and onlyTHE they are the same. Also, the plane's speed is 4 times slower than the rocket's speed. Thus:
being vF.t = sF, so the distance traveled by the rocket was approximately 5.3 km.
See too: Uniformly Varied Movement - Exercises
question 8
(Enem - 2012) A transport company needs to deliver an order as soon as possible. To do so, the logistics team analyzes the route from the company to the delivery location. She checks that the route has two sections of different distances and different maximum allowable speeds. In the first stretch, the maximum speed allowed is 80 km/h and the distance to be covered is 80 km. In the second stretch, whose length is 60 km, the maximum speed allowed is 120 km/h. Assuming that traffic conditions are favorable for the company vehicle to travel continuously at the maximum allowed speed, what will be the time needed, in hours, for the carrying out the delivery?
a) 0.7
b) 1.4
c) 1.5
d) 2.0
e) 3.0
Correct alternative: c) 1.5
To find the solution, let's calculate the time on each leg of the route.
As the vehicle will be in each stretch with the same speed, we will use the MRU formula, that is:
Therefore, it will take 1.5 h (1 + 0.5) to complete the entire journey.
See too: kinematics
question 9
(FATEC - 2018) Electronic devices placed on public roads, known as Fixed Radars (or "sparrows"), work through a set of sensors placed on the floor of these roads. Detector loops (set of two electromagnetic sensors) are placed on each bearing band. Since motorcycles and automobiles have ferromagnetic materials, when they pass through the sensors, the affected signals are processed and two speeds determined. One between the first and second sensor (1st loop); and the other between the second and third sensor (2nd loop), as shown in the figure.
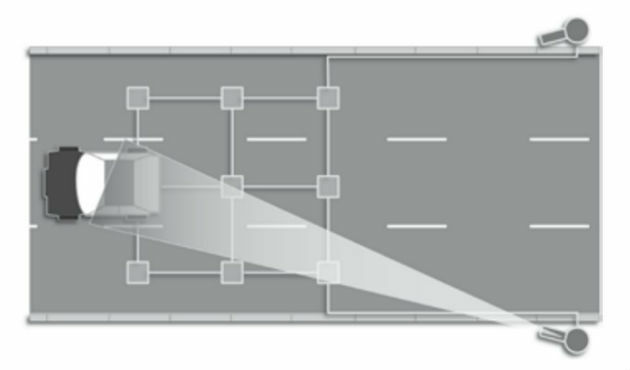
These two measured speeds are validated and correlated with the speeds to be considered (VÇ), as shown in the partial table of speed reference values for infractions (art. 218 of the Brazilian Traffic Code – CTB). If these speeds verified in the 1st and 2nd loop are equal, this value is called measured speed (VM), and it is related to the considered speed (VÇ). The camera is activated to record the image of the license plate of the vehicle to be fined only in situations where this is traveling above the maximum allowed limit for that location and rolling range, considering the values of VÇ.

Consider that, in each lane, the sensors are about 3 meters apart from each other and suppose that the car in the figure is moving to the left and passing through the first loop at a speed of 15 m/s, thus taking 0.20 s to pass through the second link. If the speed limit of this lane is 50 km/h, we can say that the vehicle
a) will not be fined, as VM is less than the minimum allowed speed.
b) will not be fined, as VÇ is less than the maximum allowed speed.
c) will not be fined, as VÇ is less than the minimum allowed speed.
d) will be fined since VM is greater than the maximum allowed speed.
e) will be fined, as VÇ is greater than the maximum allowed speed.
Correct alternative: b) will not be fined, as VÇ is less than the maximum allowed speed.
First, we need to know the measured velocity (VM) in km/h to, through the table, find the considered speed (VÇ).
To do this, we must multiply the reported speed by 3.6, like this:
15. 3.6 = 54 km/h
From the data in the table, we find that VÇ = 47 km/h. Therefore, the vehicle will not be fined, as VÇ is less than the maximum allowed speed (50 km/h).
To learn more, see also:
- Uniform Movement
- Uniform Rectilinear Movement
- Uniformly Varied Movement
- Uniformly Varied Rectilinear Movement

