Elastic strength (Fhe) is the force exerted on a body that has elasticity, for example a spring, rubber or elastic.
This force therefore determines the deformation of this body when it stretches or compresses. This will depend on the direction of the applied force.
As an example, let's think of a spring attached to a support. If there is no force acting on it, we say it is at rest. In turn, when we stretch this spring, it will create a force in the opposite direction.
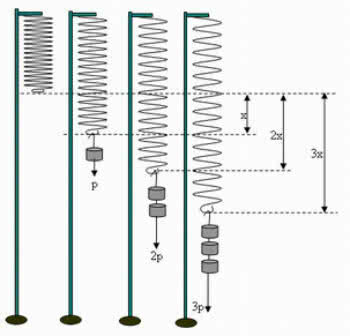
Note that the deformation suffered by the spring is directly proportional to the intensity of the applied force. Thus, the greater the applied force (P), the greater the deformation of the spring (x), as seen in the image below:
Tensile strength formula
To calculate the elastic force, we use a formula developed by the English scientist Robert Hooke (1635-1703), called Hooke's Law:
F = K. x
Where,
F: force applied to the elastic body (N)
K: elastic constant (N/m)
x: variation suffered by the elastic body (m)
Elastic constant
It is worth remembering that the so-called “elastic constant” is determined by the nature of the material used, and also by its dimensions.
Examples
1. A spring has one end fixed to a support. When applying a force at the other end, this spring undergoes a deformation of 5 m. Determine the intensity of the applied force, knowing that the spring constant is 110 N/m.
To know the strength of the force exerted on the spring, we must use the formula of Hooke's Law:
F = K. x
F = 110. 5
F = 550 N
2. Determine the variation of a spring that has an acting force of 30N and its elastic constant is 300N/m.
To find the variation suffered by the spring, we use the formula of Hooke's Law:
F = K. x
30 = 300. x
x = 30/300
x = 0.1 m
Elastic Potential Energy
The energy associated with elastic force is called elastic potential energy. It is related to the work performed by the elastic force of the body that goes from the initial position to the deformed position.
The formula for calculating elastic potential energy is expressed as follows:
EPand = Kx2/2
Where,
EPand: elastic potential energy
K: elastic constant
x: measure of elastic body deformation
Want to know more? Read too:
- Strength
- Potential energy
- Elastic Potential Energy
- Physics Formulas
Entrance Exam Exercises with Feedback
1. (CFU) A particle, with mass m, moving in a horizontal plane, without friction, is attached to a spring system in four different ways, shown below.
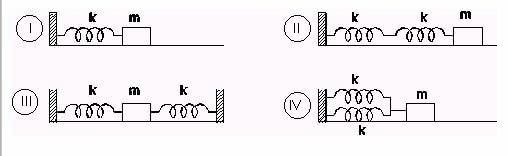
Regarding the particle oscillation frequencies, tick the correct alternative.
a) The frequencies in cases II and IV are the same.
b) The frequencies in cases III and IV are the same.
c) The highest frequency occurs in case II.
d) The highest frequency occurs in case I.
e) The lowest frequency occurs in case IV.
Alternative b) The frequencies in cases III and IV are the same.
2. (UFPE) Consider the spring-mass system in the figure, where m = 0.2 Kg and k = 8.0 N/m. The block is dropped from a distance equal to 0.3 m from its equilibrium position, returning to it with exactly zero velocity, therefore without going beyond the equilibrium position even once. Under these conditions, the coefficient of kinetic friction between the block and the horizontal surface is:
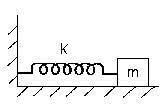
a) 1.0
b) 0.6
c) 0.5
d) 0.707
e) 0.2
Alternative b) 0.6
3. (UFPE) An object with mass M = 0.5 kg, supported on a horizontal surface without friction, is attached to a spring whose elastic force constant is K = 50 N/m. The object is pulled for 10 cm and then released, starting to oscillate in relation to the balanced position. What is the object's maximum speed, in m / s?

a) 0.5
b) 1.0
c) 2.0
d) 5.0
e) 7.0
Alternative b) 1.0