Pythagorean Theorem: Solved and Commented Exercises

Pythagoras' theorem indicates that, in a right triangle, the squared hypotenuse measure is equal to the sum of the squares of the leg measures.

Take advantage of the solved and commented exercises to answer all your doubts about this important content.

Proposed exercises (with resolution)

question 1

Carlos and Ana left home to work from the same point, the garage of the building where they live. After 1 min, following a perpendicular path, they were 13 m apart.

If Carlos' car did 7 m more than Ana's during that time, how far were they from the garage?

a) Carlos was 10 m from the garage and Ana was 5 m.
b) Carlos was 14 m from the garage and Ana was 7 m.
c) Carlos was 12 m from the garage and Ana was 5 m.
d) Carlos was 13 m from the garage and Ana was 6 m.

See Answer

Correct answer: c) Carlos was 12 m from the garage and Ana was 5 m.

The sides of the right triangle formed in this question are:

• hypotenuse: 13 m
• larger leg: 7 + x
• shorter leg: x

Applying the values ​​in Pythagoras' theorem, we have:

Now we apply Bhaskara's formula to find the value of x.

As it is a measure of length, we must use the positive value. Therefore, the sides of the right triangle formed in this question are:

• hypotenuse: 13 m
• longer leg: 7 + 5 = 12 m
• shorter leg: x = 5 m

Thus, Ana was 5 meters from the garage and Carlos was 12 meters away.

question 2

Carla when looking for her kitten saw him on top of a tree. She then asked her mother for help and they placed a ladder by the tree to help the cat down.

Knowing that the cat was 8 meters from the ground and the base of the ladder was positioned 6 meters from the tree, how long was the ladder used to save the kitten?

a) 8 meters.
b) 10 meters.
c) 12 meters.
d) 14 meters.

See Answer

Correct answer: b) 10 meters.

Note that the height the cat is at and the distance the base of the ladder has been positioned form a right angle, that is, a 90-degree angle. As the ladder is positioned opposite the right angle, then its length corresponds to the hypotenuse of the right triangle.

Applying the values ​​given in Pythagoras' theorem we discover the value of the hypotenuse.

Therefore, the ladder is 10 meters long.

question 3

According to the measures presented in the alternatives below, which presents the values ​​of a right triangle?

a) 14 cm, 18 cm and 24 cm
b) 21 cm, 28 cm and 32 cm
c) 13 cm, 14 cm and 17 cm
d) 12 cm, 16 cm and 20 cm

See Answer

Correct answer: d) 12 cm, 16 cm and 20 cm.

To find out if the measures presented form a right triangle we must apply the Pythagorean theorem for each alternative.

a) 14 cm, 18 cm and 24 cm

b) 21 cm, 28 cm and 32 cm

c) 13 cm, 14 cm and 17 cm

d) 12 cm, 16 cm and 20 cm

Therefore, the measures 12 cm, 16 cm and 20 cm correspond to the sides of a right triangle, as the square of the hypotenuse, the longest side, is equal to the sum of the square of the legs.

question 4

Note the following geometric figures, which have one side located in the hypotenuse of a right triangle measuring 3 m, 4 m and 5 m.

Find the height (h) of the equilateral triangle BCD and the diagonal value (d) of the square BCFG.

a) h = 4.33 m and d = 7.07 m
b) h = 4.72 m and d = 8.20 m
c) h = 4.45 m and d = 7.61 m
d) h = 4.99 m and d = 8.53 m

See Answer

Correct answer: a) h = 4.33 m and d = 7.07 m.

As the triangle is equilateral, it means that its three sides have the same measure. By drawing a line that corresponds to the height of the triangle, we split it into two right triangles.

The same is true with the square. When we draw its diagonal line, we can see two right triangles.

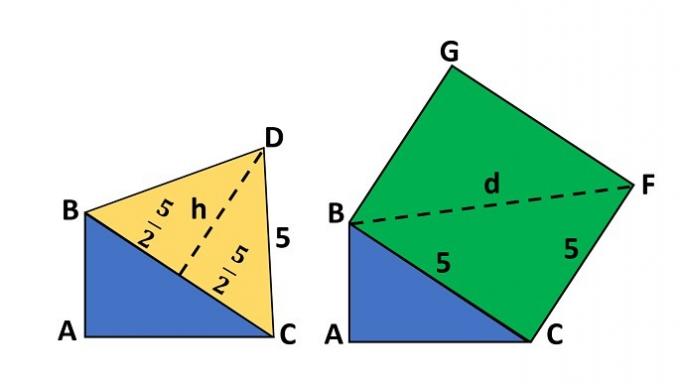
Applying the data from the statement in Pythagoras' theorem, we find the values ​​as follows:

1. Calculating the height of the triangle (right triangle leg):

We then arrive at the formula for calculating height. Now, just substitute the value of L and calculate it.

2. Calculation of the diagonal of the square (hypotenuse of the right triangle):

Therefore, the height of the equilateral triangle BCD is 4.33 and the diagonal value of the square BCFG is 7.07.

See too: Pythagorean theorem

Entrance Exam Issues Resolved

question 5

(Cefet/MG - 2016) A kite, whose figure is shown below, was built in the ABCD quadrilateral format, being and . the stick of the kite intersects the rod at its midpoint E, forming a right angle. In the construction of this kite, the measures of used are, respectively, 25 cm and 20 cm, and the measurement of equals of the measure of .

Under these conditions, the measure of , in cm, is equal to

a) 25.
b) 40.
c) 55.
d) 70.

See Answer

Correct alternative: c) 55.

Looking at the figure in the question, we see that the DE segment, which we want to find, is the same as the BD segment by subtracting the BE segment.

So, as we know that segment BE is equal to 20 cm, then we need to find the value of segment BD.

Note that the problem gives us the following information:

So to find the measure of BD, we need to know the value of the segment AC.

Since point E divides the segment into two equal parts (midpoint), then . Therefore, the first step is to find the CE segment measure.

To find the CE measurement, we identified that the triangle BCE is a rectangle, that BC is the hypotenuse and BE and CE are the legs, as shown in the image below:

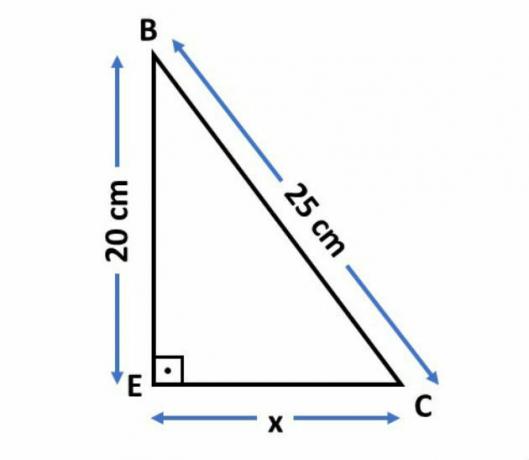
We will then apply Pythagoras' theorem to find the measure of the leg.

25² = 20²+x²
625 = 400 + x²
x² = 625 - 400
x² = 225
x = √225
x = 15 cm

To find the collar, we could also have observed that the triangle is Pythagorean, that is, the measurements of its sides are multiple numbers of the measurements of the triangle 3, 4, 5.

Thus, when we multiply 4 by 5 we have the value of the collar (20) and if we multiply 5 by 5 we have the hypotenuse (25). Therefore, the other leg could only be 15 (5. 3).

Now that we have found the EC value, we can find the other measures:

AC = 2. CE ⇒ AC = 2.15 = 30 cm

Therefore, the measure of is equal to 55 cm.

See too: Pythagoras

question 6

(IFRS - 2017) Consider an equilateral triangle with a 5√3 ܿ݉ side. What is the height and area of ​​this triangle, respectively?

See Answer

Correct alternative: e) 7.5 cm and 75√3/4 cm²

First, let's draw the equilateral triangle and plot the height, as shown in the image below:

Note that the height divides the base into two segments of the same measure, as the triangle is equilateral. Also note that triangle ACD in the figure is a right triangle.

Thus, to find the height measure, we will use the Pythagorean theorem:

Knowing the height measurement, we can find the area through the formula:

question 7

(IFRS - 2016) In the figure below, the value of x and y, respectively, is

See Answer

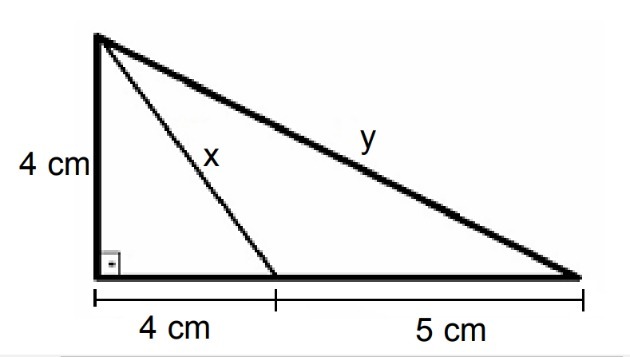
Correct alternative: a) 4√2 and √97.

To find the value of x, let's apply Pythagoras' theorem to the right triangle that has sides equal to 4 cm.

x² = 4² + 4²
x² = 16 + 16
x = √32
x = 4√2 cm

To find the value of y, we will also use Pythagoras' theorem, now considering that one leg measures 4 cm and the other 9 cm (4 + 5 = 9).

y² = 4² + 9²
y² = 16 + 81
y = √97 cm

Therefore, the value of x and y, respectively, is 4√2 and √97.

question 8

(Apprentice Sailor - 2017) Look at the figure below.

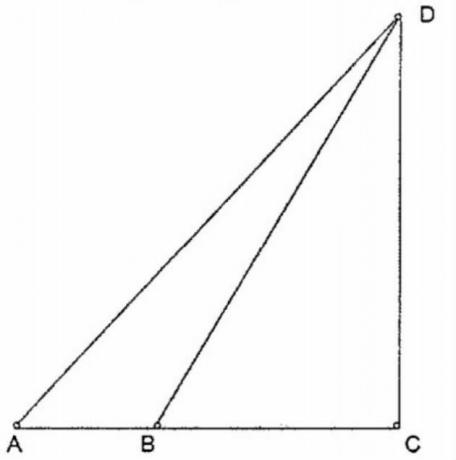
In the figure above, there is an isosceles triangle ACD, in which the segment AB measures 3 cm, the unequal side AD measures 10√2 cm, and the segments AC and CD are perpendicular. Therefore, it is correct to state that the BD segment measures:

a) √53 cm
b) √97 cm
c) √111 cm
d) √149 cm
e) √161 cm

See Answer

Correct alternative: d) √149 cm

Considering the information presented in the problem, we build the figure below:

According to the figure, we find that to find the value of x, it will be necessary to find the measure of the side we call a.

Since the triangle ACD is a rectangle, we will apply Pythagoras' theorem to find the value of the leg a.

Now that we know the value of a, we can find the value of x by considering the right triangle BCD.

Note that the leg BC is equal to the measurement of the leg minus 3 cm, that is, 10 - 3 = 7 cm. Applying Pythagoras' theorem to this triangle, we have:

Therefore, it is correct to state that the BD segment measures √149 cm.

question 9

(IFRJ - 2013) The sports yard of the Arrozal Campus of a Federal Institute is rectangular, 100 m long and 50 m wide, represented by the ABCD rectangle in this figure.

Alberto and Bruno are two students, who are playing sports in the courtyard. Alberto walks from point A to point C along the diagonal of the rectangle and returns to the starting point along the same path. Bruno starts from point B, goes around the yard completely, walking along the side lines, and returns to the starting point. Thus, considering √5 = 2.24, it is stated that Bruno walked more than Alberto

a) 38 m.
b) 64 m.
c) 76 m.
d) 82 m.

See Answer

Correct alternative: c) 76 m.

The rectangle's diagonal divides it into two right triangles, the hypotenuse being the diagonal and the sides equal to the sides of the rectangle.

So, to calculate the diagonal measure, let's apply the Pythagorean theorem:

Whereas Alberto went and came back, so he covered 224 m.

Bruno covered a distance equal to the perimeter of the rectangle, in other words:

p = 100 + 50 + 100 + 50
p = 300 m

Therefore, Bruno walked 76 m longer than Alberto (300 - 112 = 76 m).

question 10

(Enem - 2017) To decorate a children's party table, a chef will use a spherical melon with a diameter measuring 10 cm, which will serve as a support to skewer various sweets. It will remove a spherical hubcap from the melon, as shown in the figure, and, to ensure the stability of this support, making it difficult for the melon to roll on the table, the boss will cut so that the radius r of the circular cut section is hairy. minus 3 cm. On the other hand, the chef will want to have the largest possible area in the region where the sweets will be fixed.

To achieve all his goals, the boss must cut the melon cap at a height h, in centimeters, equal to

See Answer

Correct alternative: c) 1

Observing the figure presented in the question, we identified that the height h can be found by decreasing the measure of the segment OA from the measure of the radius of the sphere (R).

The radius of the sphere (R) is equal to half its diameter, which in this case is equal to 5 cm (10: 2 = 5).

So we need to find the value of the OA segment. For this, we will consider the triangle OAB represented in the figure below and apply the Pythagorean theorem.

5² = 3² + x²
x² = 25 - 9
x = √16
x = 4 cm

We could also find the value of x directly, noting that it is the Pythagorean triangle 3,4 and 5.

So the value of h will be equal to:

h = R - x
h = 5 - 4
h = 1 cm

Therefore, the chef should cut the melon cap at a height of 1 cm.

question 11

(Enem - 2016 - 2nd application) Boccia is a sport played on courts, which are flat and level terrain, limited by perimeter wooden platforms. The objective of this sport is to throw boules, which are balls made of a synthetic material, in order to place them as close as possible to the bolim, which is a smaller ball, preferably made of steel, previously launched. Figure 1 illustrates a bocce ball and a bolim that were played on a court. Suppose that a player has thrown a ball, with a radius of 5 cm, which has been leaning against the bollin, with a radius of 2 cm, as shown in figure 2.

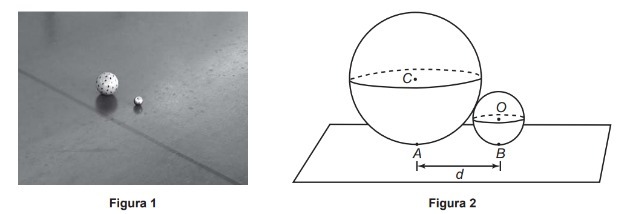
Consider point C as the center of the ball, and point O as the center of the ball. It is known that A and B are the points at which the bocce ball and the bollin, respectively, touch the ground of the court, and that the distance between A and B is equal to d. Under these conditions, what is the ratio between d and the radius of the bolim?

See Answer

Correct alternative: e) √10

To calculate the value of the distance d between points A and B, let's build a figure joining the centers of the two spheres, as shown below:

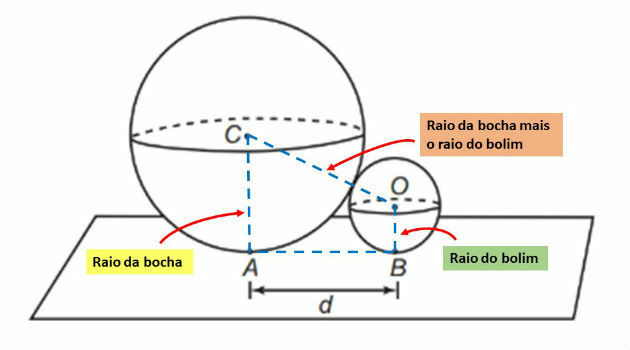
Note that the blue dotted figure is shaped like a trapeze. Let's divide this trapeze, as shown below:

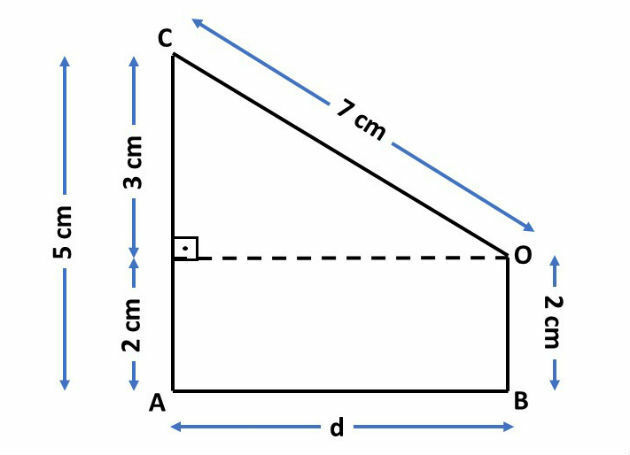
By splitting the trapeze, we get a rectangle and a right triangle. The hypotenuse of the triangle is equal to the sum of the radius of the bocce ball with the radius of the bolim, that is, 5 + 2 = 7 cm.

The measurement of one of the legs is equal to d and the measurement of the other leg is equal to the measurement of the segment CA, which is the radius of the bocce ball, minus the radius of the bolim (5 - 2 = 3).

In this way, we can find the measure of d, applying the Pythagorean theorem to this triangle, that is:

7² = 3² - of²
d² = 49 - 9
d = √40
d = 2 √10

Therefore, the ratio between the distance d and the bolim will be given by:.

question 12

(Enem - 2014) Daily, a residence consumes 20 160 Wh. This residence has 100 solar cells rectangular (devices capable of converting sunlight into electrical energy) measuring 6 cm x 8 cm. Each such cell produces, throughout the day, 24 Wh per centimeter of diagonal. The owner of this house wants to produce, per day, exactly the same amount of energy that his house consumes. What should this owner do for him to achieve his goal?

a) Remove 16 cells.
b) Remove 40 cells.
c) Add 5 cells.
d) Add 20 cells.
e) Add 40 cells.

See Answer

Correct alternative: a) Remove 16 cells.

First, you will need to find out what the energy output of each cell is. For that, we need to find the measure of the rectangle's diagonal.

The diagonal is equal to the hypotenuse of the triangle with legs equal to 8 cm and 6 cm. We will then calculate the diagonal by applying the Pythagorean theorem.

However, we observe that the triangle in question is Pythagorean, being a multiple of triangle 3,4 and 5.

In this way, the measurement of the hypotenuse will be equal to 10 cm, as the sides of the Pythagorean triangle 3,4 and 5 are multiplied by 2.

Now that we know the diagonal measurement, we can calculate the energy produced by the 100 cells, ie:

E = 24. 10. 100 = 24 000 Wh

As the energy consumed is equal to 20 160 Wh, we will have to reduce the number of cells. To find this number we will do:

24 000 - 20 160 = 3 840 Wh

Dividing this value by the energy produced by a cell, we find the number that should be reduced, that is:

3 840: 240 = 16 cells

Therefore, the owner's action for him to achieve his goal should be to remove 16 cells.

To learn more, see also: Trigonometry Exercises