Prime Numbers are natural numbers greater than 1 that have only two divisors, that is, they are divisible by 1 and by itself.
The Fundamental Theorem of Arithmetic is part of the "Theory of Numbers" and guarantees that every larger natural number that 1 is either prime or can be written uniquely, except for the order of the factors, as the product of numbers cousins.
To write a number as a product of prime numbers or "prime factors", we use a number decomposition process called factorization.
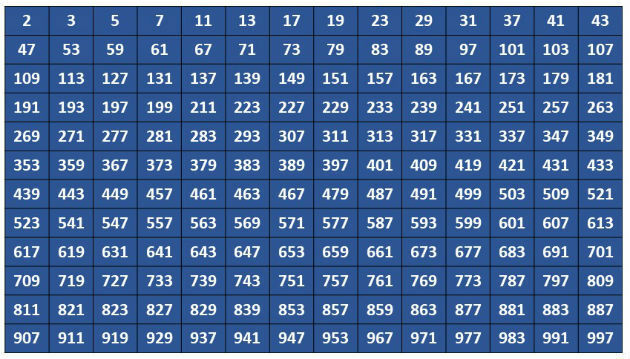
Prime numbers between 1 and 1000
Between 1 and 1000 there are 168 prime numbers, they are:
Factorization
THE factorization corresponds to the decomposition of numbers into prime factors, for example:
3 = 3 x 1
4 = 2 x 2
8 = 2 x 2 x 2
9 = 3 x 3
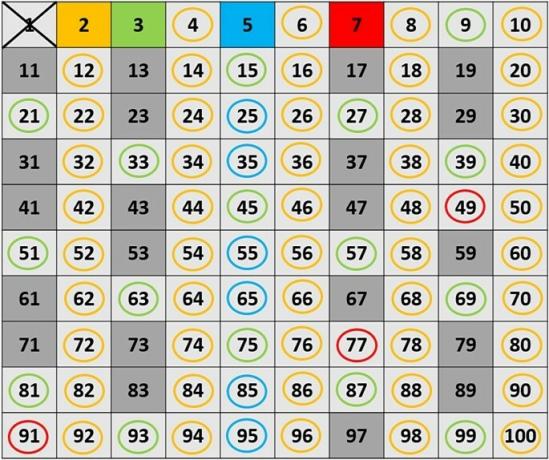
Sieve of Eratosthenes
Eratosthenes (285-194 a. C.) was a Greek mathematician who discovered a scheme for finding prime numbers that became known as the "Riddle of Eratosthenes".
This scheme is represented through a table composed of natural numbers. Thus, the method used is to first find the first prime number in the table, mark all multiples of that number, and repeat this operation until the last one.
This way, only the prime numbers will remain in the table, as shown in the figure below:

Read: What are prime numbers?
Encryption and Prime Numbers
Encryption is used for the secure transmission of sensitive data and information through communication channels.
With the growing use of the internet as a medium for financial and commerce transactions, encryption becomes increasingly important to ensure the security of information.
One of the most used encryption methods is RSA. It is based on the fact that it is very difficult and time-consuming to factor large numbers into prime factors.
To learn more about this topic, watch the video on the relationship between prime numbers and internet safety.
Curiosities
- The word "cousin" refers to "first".
- The number 2 is the only even prime number.
- The number 1 is not a prime number as it has only one divisor.
- The largest known prime number is 24,862,048 digits long and was discovered by Patrick Laroche of Ocala on December 7, 2018, in Florida, United States.
- In 2013, the Peruvian Harald Andrés Helfgott solved a problem with prime numbers, called the "weak conjecture" that had been unsolved since the end of the 18th century.
See too:
- Integers
- Natural Numbers
- real numbers
- Rational Numbers
- multiplication tables
- MMC and MDC - Exercises
- divisibility criteria