Newton's Third Law: Concept, Examples and Exercises

Newton's Third Law, also called Action and Reaction, relates the forces of interaction between two bodies.

When an object A exerts a force on another object B, this other object B will exert a force of the same intensity, same direction and opposite direction on object A.

As the forces are applied to different bodies, they do not balance.

Examples:

• When firing a shot, a shooter is propelled away from the bullet by a firing reaction force.
• In a collision between a car and a truck, both receive the action of forces of the same intensity and opposite direction. However, we found that the action of these forces in the deformation of vehicles is different. Usually the car is much more "crushed" than the truck. This fact occurs because of the difference in the structure of the vehicles and not because of the difference in the intensity of these forces.
• The Earth exerts an attractive force on all bodies near its surface. According to Newton's 3rd Law, bodies also exert an attractive force on the Earth. However, due to the difference in mass, we find that the displacement suffered by bodies is much more considerable than that suffered by the Earth.
• Spaceships use the principle of action and reaction to move. When ejecting combustion gases, they are driven in the opposite direction from the exits of these gases.

The ships move by ejecting combustion gases

Application of Newton's 3rd Law

Many situations in the study of Dynamics present interactions between two or more bodies. To describe these situations we apply the Law of Action and Reaction.

By acting in different bodies, the forces involved in these interactions do not cancel each other out.

As the force is a vector quantity, we must first vectorally analyze all the forces acting on each body that makes up the system, marking the action and reaction pairs.

After this analysis, we established the equations for each involved body, applying Newton's 2nd Law.

Example:

Two blocks A and B, with masses respectively equal to 10 kg and 5 kg, are supported on a perfectly smooth horizontal surface, as shown in the figure below. A constant and horizontal force of intensity 30N acts on block A. Determine:

a) the acceleration acquired by the system
b) the intensity of the force that block A exerts on block B

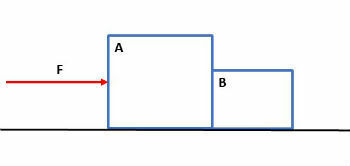
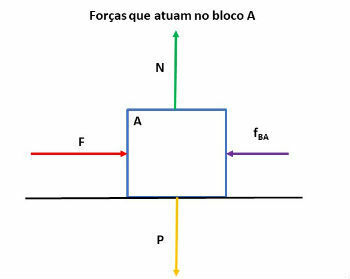
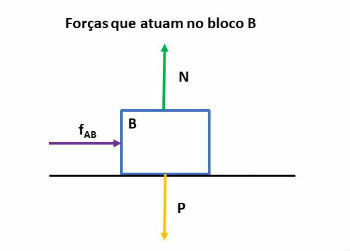
First, let's identify the forces acting on each block. To do this, we isolated the blocks and identified the forces, as shown in the figures below:

Being:

f_AB: force block A exerts on block B
f_BA: force block B exerts on block A
N: normal force, that is, the contact force between the block and the surface
P: strength weight

The blocks do not move vertically, so the net force in this direction is equal to zero. Therefore, normal weight and strength cancel each other out.

On the horizontal, the blocks show movement. So let's apply Newton's 2nd Law (F_R = m. a) and write the equations for each block:

Block A:

F - f_BA = m_THE. The

Block B:

f_AB = m_B. The

Putting these two equations together, we find the system equation:

F - f_BA+ f_AB= (m_THE. a) + (m_B. The)

As the intensity of f_AB equals the intensity of f_BA, since one is the reaction to the other, we can simplify the equation:

F = (m_THE + m_B). The

Replacing the given values:

30 = (10 + 5). The

Now, we can find the value of the force that block A exerts on block B. Using the block B equation, we have:

f_AB = m_B. The
f_AB = 5. 2 = 10 N

Newton's Three Laws

the physicist and mathematician Isaac Newton (1643-1727) formulated the basic laws of mechanics, where he describes the movements and their causes. The three laws were published in 1687, in the work "Mathematical Principles of Natural Philosophy".

The 3rd Law, together with two other laws (1st Law and 2nd Law) form the foundations of Classical Mechanics.

Newton's First Law

THE Newton's First Law, also called the Law of Inertia, states that "a body at rest will remain at rest and a body in motion will remain in motion unless it is influenced by an external force".

In summary, Newton's First Law points out that it takes the action of a force to change the state of rest or motion of a body.

Also read about Galileo Galilei.

Newton's Second Law

THE Newton's 2nd Law establishes that the acceleration acquired by a body is directly proportional to the resultant of the forces acting on it.

It is expressed mathematically by:

To learn more, read also:

• Newton's Laws
• Gravity
• Physics Formulas

Solved Exercises

1) UFRJ-1999

Block 1, of 4 kg, and block 2, of 1 kg, shown in the figure, are juxtaposed and supported on a flat, horizontal surface. They are accelerated by force horizontal, with a modulus equal to 10 N, applied to block 1 and they start to slide on the surface with negligible friction.

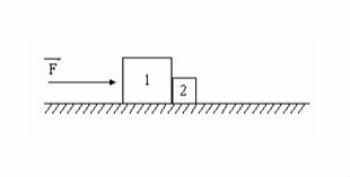
a) Determine the direction and direction of the force F₁₂ exercised by block 1 on block 2 and calculate its modulus.
b) Determine the direction and direction of force F₂₁ exercised by block 2 on block 1 and calculate its modulus.

See Answer

a) Horizontal direction, left to right direction, module f₁₂ = 2 N
b) Horizontal direction, right to left direction, module f₂₁ = 2 N

2) UFMS-2003

Two blocks A and B are placed on a flat, horizontal and frictionless table as shown below. A horizontal force of intensity F is applied to one of the blocks in two situations (I and II). As the mass of A is greater than that of B, it is correct to state that:

a) the acceleration of block A is smaller than that of B in situation I.
b) the acceleration of the blocks is greater in situation II.
c) the contact force between the blocks is greater in situation I.
d) the acceleration of the blocks is the same in both situations.
e) the contact force between the blocks is the same in both situations.

See Answer

Alternative d: The acceleration of the blocks is the same in both situations.