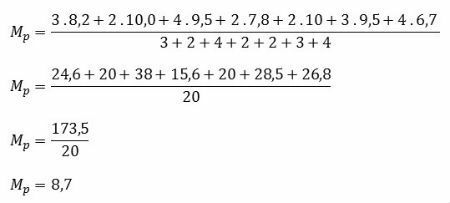Perfect Square: what is it, how to calculate, examples and rules

A perfect square or perfect square number is a natural number that, if rooted, results in another natural number.

That is, they are the result of the operation of a number multiplied by itself.

Example:

• 1 × 1 = 1
• 2 × 2 = 4
• 3 × 3 = 9
• 4 × 4 = 16
  (...)

The perfect square formula is represented by: n × n = a or no² = the. Thus, no is a natural number and The is a perfect square number.

What are perfect square numbers?

The definition of a perfect square number can be understood as: a positive integer natural number whose square root is also a positive integer natural number.

So we have: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100...

√1 = 1, √4 = 2, √9 = 3, √16 = 4, √25 = 5, √36 =6, √49 = 7, √64 = 8, √81 = 9, √100 = 10...

Multiplication table and cueing of perfect square numbers up to 15

If we take geometry as a basis, we can think that a square is the figure that has sides with the same measure.

So the area of ​​the square is l × l or l ².

Every square whose sides are whole numbers will be perfect squares.

Examples of squares: 1² = 1 and 4² = 16

How to calculate if a number is a perfect square?

From the factorization of a number, if it has an exact square root and if it is the result of the square of other numbers, we can say that it is a perfect square.

Example:

2704 is a perfect square?

To answer the question, it is necessary to factor 2704, that is, calculate .

Hence, we have: 2704 = 2 × 2 × 2 × 2 × 13 × 13 = 2⁴ × 13^{2 .}

√2704 = √(2² × 2² ×13²⁾ = 2 × 2 × 13 = 52

2704 is the perfect square number of 52.

perfect square rules

• A perfect square number is one that has an exact root.
• An odd perfect square number has its odd root and an even has an even root.
• Perfect square numbers never end with the digits 2, 3, 7, and 8.
• Numbers ending 0 have squares ending 00.
• Numbers ending in 1 or 9 have squares ending in 1.
• Numbers ending in 2 or 8 have squares ending in 4.
• Numbers ending in 3 or 7 have squares ending in 9.
• Numbers ending in 4 or 6 have squares ending in 6.
• Numbers ending 5 have squares ending 25

other relationships

The square of a number is equal to the product of its adjacent ones plus one. For example: the square of seven (7²) is equal to the product of their adjacent numbers (6 and 8) plus one. 7² = 6 × 8 + 1 = 48 + 1 = 49. x² = (x-1).(x+1) + 1.

Perfect squares are the result of a mathematical succession between the previous perfect square and an arithmetic progression.

1² = 1
2² = 1 + 3 = 4
3² = 4 + 5 = 9
4² = 9 + 7 = 16
5² = 16 + 9 = 25
6² = 25 + 11 = 36
7² = 36 + 13 = 49
8² = 49 + 15 = 64
9² = 64 + 17 = 81
10² = 81 + 19 = 100...

See too:

• Square Root Calculation
• Potentiation
• Radiation