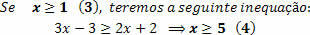Proportionality establishes a relationship between quantities and quantity is everything that can be measured or counted.
In everyday life there are many examples of this relationship, such as when driving a car, the time it takes to taking the route depends on the speed used, that is, time and speed are magnitudes proportional.
What is proportionality?
A ratio represents the equality between two ratios, with a ratio corresponding to the quotient of two numbers. See how to represent it below.
It reads: a is to b as c is to d.
Above, we see that a, b, c and d are the terms of a proportion, which has the following properties:
-
fundamental property:
-
property of sum:
-
Subtraction property:
Example of proportionality: Pedro and Ana are brothers and they realized that the sum of their ages is equal to their father's age, which is 60 years old. If Peter's age is to Anna's as 4 is to 2, how old are each of them?
Solution:
First, we set up the proportion using P for Pedro's age and A for Ana's age.
Knowing that P + A = 60, we apply the sum property and find Ana's age.
Applying the fundamental property of proportions, we calculate Peter's age.
We found out that Ana is 20 years old and Pedro is 40 years old.
know more about Ratio and Proportion.
Proportionalities: direct and inverse
When we establish the relationship between two quantities, the variation of one quantity causes a change in the other quantity in the same proportion. There is then a direct or inverse proportionality.
Directly proportional quantities
Two quantities are directly proportional when the variation always occurs in the same ratio.
Example: An industry has installed a level gauge, which every 5 minutes measures the height of water in the reservoir. Observe the variation in water height over time.
| Time (min) | Height (cm) |
| 10 | 12 |
| 15 | 18 |
| 20 | 24 |
Note that these quantities are directly proportional and have linear variation, that is, an increase in one implies an increase in the other.
THE proportionality constant (k) establishes a ratio between the numbers of the two columns as follows:
Generically, we can say that the constant for directly proportional quantities is given by x/y = k.
Inversely proportional quantities
Two quantities are inversely proportional when one quantity varies in inverse ratio to the other.
Example: João is training for a running test and therefore decided to check the speed he should run to reach the finish line in the shortest time possible. Note the time it took at different speeds.
| Speed (m/s) | Time(s) |
| 20 | 60 |
| 40 | 30 |
| 60 | 20 |
Note that the quantities vary inversely, that is, an increase in one implies a decrease in the other in the same proportion.
See how it is given to proportionality constant (k) between the magnitudes of the two columns:
Generically, we can say that the constant for inversely proportional quantities is found using the formula x. y = k.
Read too: Magnitudes directly and inversely proportional
Proportional magnitude exercises (with answers)
question 1
(Enem/2011) It is known that the real distance, in a straight line, from a city A, located in the state of São Paulo, to a city B, located in the state of Alagoas, is equal to 2,000 km. A student, when analyzing a map, verified with his ruler that the distance between these two cities, A and B, was 8 cm. The data indicate that the map observed by the student is on the scale of:
a) 1:250
b) 1:2500
c) 1:25000
d) 1:250000
e) 1:25000000
Correct alternative: e) 1:25000000.
Statement data:
- Actual distance between A and B is equal to 2 000 km
- Distance on the map between A and B is equal to 8 cm
On a scale the two components, actual distance and distance on the map, must be in the same unit. Therefore, the first step is to transform km into cm.
2 000 km = 200 000 000 cm
On a map, the scale is given as follows:
Where, the numerator corresponds to the distance on the map and the denominator represents the actual distance.
To find the value of x we make the following proportion between the quantities:
To calculate the value of X, we apply the fundamental property of proportions.
We came to the conclusion that the data indicate that the map observed by the student is in the scale of 1:25000000.
See too: Exercises on Ratio and Proportion
question 2
(Enem / 2012) A mother used the package insert to check the dosage of a drug she needed to give her child. In the package insert, the following dosage was recommended: 5 drops for each 2kg of body weight every 8 hours.
If the mother correctly administered 30 drops of the medicine to her child every 8 hours, then his body mass is:
a) 12 kg.
b) 16 kg.
c) 24 kg.
d) 36 kg.
e) 75 kg.
Correct alternative: a) 12 kg.
First, we set up the proportion with the utterance data.
We then have the following proportionality: 5 drops should be given to every 2 kg, 30 drops were given to a person of mass X.
Applying the fundamental theorem of proportions, we find the child's body mass as follows:
So, 30 drops were given because the child is 12 kg.
Get more knowledge by reading a text about Simple and Compound Three Rule.