A quadrilateral can be circumscribed to a circle if there is a tangency between its sides and the circumference. Look at the figure below:
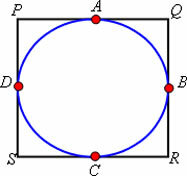
In these cases of quadrilaterals circumscribed to the circumference, some properties are used in the calculation of segment measurements.
If we add the opposite sides of the circumscribed quadrilaterals to a circle, we will verify that the results are equal, that is, they have the same measure.
PQ + SR = QR + PS
Example 1
Let's determine the value of x in the figure involving a quadrilateral circumscribed to a circle.
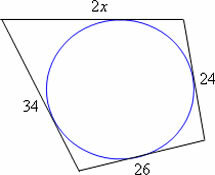
2x + 26 = 34 + 24
2x = 34 + 24 - 26
2x = 58 - 26
2x = 32
x = 32/2
x = 16
Example 2
Determine the measurement of the sides of the quadrilateral circumscribed to the circumference according to the figure below.
Do not stop now... There's more after the advertising ;)

4x + 8x – 12 = 12x – 44 + 4x + 8
4x + 8x – 12x – 4x = – 44 + 8 + 12
– 4x = – 24
4x = 24
x = 4/4
x = 6
4x = 4 * 6 = 24
8x – 12 = 8 * 6 – 12 = 48 – 12 = 36
12x – 44 = 12 * 6 – 44 = 72 – 44 = 28
4x + 8 = 4 * 6 + 8 = 24 + 8 = 32
by Mark Noah
Graduated in Mathematics
Brazil School Team
plane geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Relationship between a Quadrilateral and a Circumference"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/relacao-entre-um-quadrilatero-uma-circunferencia.htm. Accessed on June 28, 2021.