triangles are polygons that have three sides, so also present three internal angles, three external angles and three vertices. However, it is not just any three line segments that determine a triangle, that is, the size of the sides has an influence on its existence.
We can to rank you triangles according to the size of your sides, can be scalenes, isosceles or equilateral. And, in relation to your angles internal, can be called triangles rectangles, sharp angles or obtuse.

Read too: knowing the polygons
Elements of a triangle
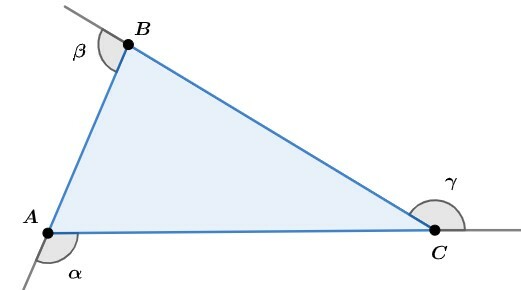
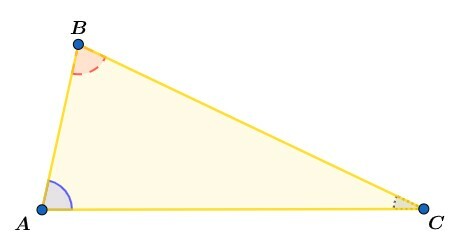
Before classifying a triangle, let's understand the elements that make it up. In every triangle we will have three sides, these are formed by straight segments. We will also have three vertices, where the line segments meet at angles internal and external. See the picture:
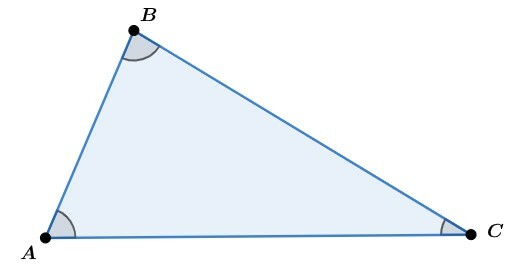
You sides, as said, they will be determined by line segments, and we will represent them as follows:
You vertices of the triangle are points where the sides meet, as well as used to name the triangle. Let's represent them like this:
You inner angles are the measurements between the sides of the triangle, so we will have three internal angles. These are represented like this:
We must place a caret (or a “hat”) on the vertex where the angle is located.
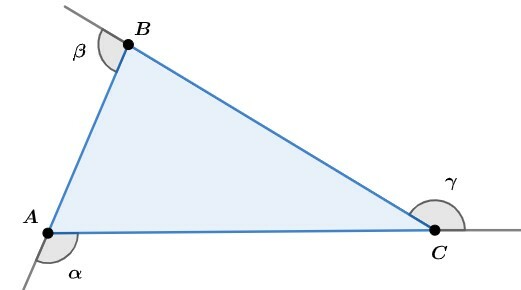
You outside angles are angles supplementary adjacent to the internal angles, and here they are represented by the Greek letters α (alpha) β (beta) and γ (gamma). See better in the image:
Know more: Sum of the interior angles of a triangle
Condition of existence of triangles
Imagine 3 straight line segments measuring respectively 10 cm, 7 cm and 6 cm. Will it be possible to build a triangle with these measurements? Watch:
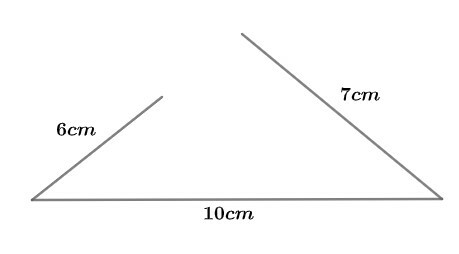
We have an example that shows that it's not any 3 segments that form a triangle. there is a condition that has to be satisfied.
The measurement on each side of the triangle should be smaller that the sum of the measure of the other two sides and, at the same time, bigger that the module of the difference between them.
The measures l1, there2 and there3 are the sizes of the sides of the triangle. This relationship is also known as triangular inequality.
- Example.
Is it possible to build a triangle with sides measuring 12 cm, 9 cm and 4 cm?
Solution:
Taking:
Note that these values satisfy the existence condition formula. Replacing the values, we have:
Like 8 < 9 < 16,then it's possible to construct a triangle with these measurements sideways.
If you want to know more about the topic, read our text: Condition of existence of a triangle.
Classification by sides
In relation to side size of a triangle, we can classify them into three: scalene triangle, isosceles triangle and equilateral triangle.
scalene triangle
We say that a triangle is scalene when all sides have different measurements.
So we can say that all internal angles are also different each other.
isosceles triangle
We say that a triangle is isosceles When two of its sides are congruent, that is, they have the same measurement, and the third side is different.

In the isosceles triangle, we also have twoequal angles, which are called base angles, it's the another different angle.
Equilateral triangle
We say that a triangle is equilateral When all your sides are the same, that is, all sides have the same measurement.

In the equilateral triangle, all angles are congruent, that is, all angles are equal. Also, a very important property of the equilateral triangle is that all your angles measure 60°.
See too: Triangles Similarity: Learn the Cases
Angle rating
Regarding the measurement of angles, we can also classify triangles into three types: right triangle, acute triangle and obtuse triangle.
rectangle triangle
When a triangle has a straight angle, it will be called right triangle. The side opposite the right angle is called hypotenuse, and the other two sides are called peccaries. Furthermore, it is for this triangle that the Pythagorean theorem.

From the previous right triangle, we can say:
m (Â) = 90º → right angle
BC → hypotenuse
AB and AC → legs
Acute Triangle
a triangle will be said sharp-angle When all yours angles internal are less than 90°.

From the acute-angled triangle, we have to:
obtuse triangle
the triangle is obtuse angle when presents a larger internal angle what 90°.

From the obtuse triangle, it follows that:
Know more: Perimeter of the equilateral triangle: learn the formula
solved exercises
Question 1. In the following figures, rank the triangles in relation to the sides and angles.
The)
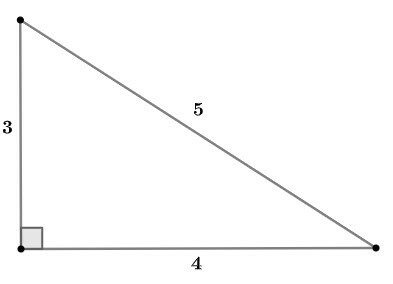
R: Rectangle and scalene
B)
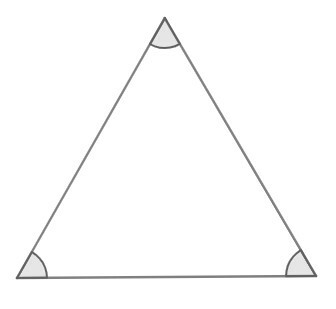
A: Acuteangle and equilateral
ç)
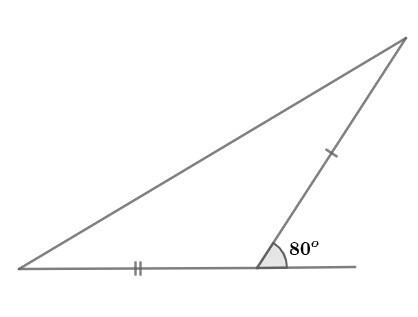
R: Obtuse angle and scalene
d)

A: Acuteangle and scalene
and)

A: Acuteangle and isosceles