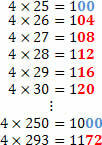Understanding the criterion of divisibility by 4 is very easy: we will have to analyze only the last two digits of the number to be divided by 4.
However, a number that is divisible by 4 is also divisible by 2, for the simple fact that 2 divides the number 4. Therefore, we can state that for a number to be divisible by the number four, we must have an even number. But this fact alone does not ensure divisibility, so we will look at its last two digits as well.
See what happens with the multiples of the number 4, after the tens places:
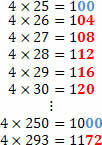
Can you identify any pattern for the last two digits of the multiples of the number 4? Note that the last two digits are always numbers divisible by 4.
Therefore, we should only analyze the divisibility of the last two digits. The special case only occurs for numbers ending with two or more zeros (100, 200,..., 1000,..., 10000, ...), in these cases they are also divisible by 4.
Therefore, we can say that:
"Numbers divisible by 4 are those in which their last two digits are divisible by 4, or are ending in 00"
Let's look at some examples.
Make sure the following numbers are divisible by 4:
a) 3659 b) 240
a) To verify the divisibility of the number 3659 by the number 4, we must analyze whether its last two digits together are divisible by 4. Therefore, for 3659 to be divisible by 4, the number 59 must be divisible by 4. Note that 59 is an odd number and no odd number can be divisible by 4, so the number 3659 is not divisible by 4.
b) Applying the divisibility criterion in the number 240, note that the last two digits form the number 40. We know that 40 is a multiple of the number 4, therefore, by the criterion of divisibility by 4, we can say that 240 is divisible by 4.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Kids School Team