Coneit's a geometric figure formed by the union of a circular region with a point that does not belong to that plane. We can also see it as revolution solid, that is, turning a triangle rectangle around their legs, a cone is formed in space.
Although they refer us to pyramids, we will see that cones do not have as many elements as they do, for example: edges, apothemas or face areas.
Read too: Dimensions of a geometric solid: learn what they are
What is a cone?
Consider a circle A contained in a plane and a point P that does not belong to that plane. Based on this, a cone is the union of all segments with ends at A and P..

Icon elements
Consider the following cone to look at its elements.
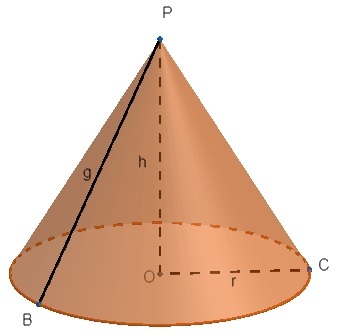
- Cone base: circle of the plane with center O and radius r.
- Cone vertex: point P.
- Cone height: h, distance between cone apex and base. Remember that height is always perpendicular to the plane containing the base, ie the angle between height and base must be 90°.
- Generatrix: g, any line segment that joins the vertex to one of the ends of the base circumference.
Classification of cones
The cones are classified into two groups: straight cones and oblique cones. Let's say that a cone is straight when the projection of its apex coincides with the center of the base, that is, with the center of the circumference, see the image.

In the straight cone, note that the measurements of the generatrix are always equal and see that POB forms a right triangle, therefore, in it the Pythagorean theorem its valid.
(PB)2 = (PO)2 + (OB)2
g2 = h2 + r2
Otherwise, the cone is called oblique.
When, in a straight cone, the triangle formed inside it is equilateral, it is about a equilateral cone, and the value of the generatrix is twice the radius, that is:
g = 2 · r
cone area
The area of the cone is determined based on the solid planning, and, just like in the pyramids, the total area of the solid is given by the sum of the lateral area (Athere) with the base area (AB), thus:

As the base is a circle, its area is:
THEB = π. r2
In it r is the measure of the lightning r of the circumference.
The lateral area is a circular sector and can be found in two ways, see:
Side area depending on the angle of the circular sector
THEthere = θ. g2
2
In it the angle q is the central angle of the sector measured in radians and g is the measure of the generatrix.

Side area as a function of the arc length of the circular sector
THEthere = π. a. g
In it r is the measure of the radius of the lateral area, and g, the measure of the generatrix.
Therefore, the area of the cone is given by:
THEcone = AB + Athere
THEcone = pir2 + πrg
THEcone = πr (g + r)
cone volume
The cone volume also depends on the base area and the height of the cone, see:

The cone volume formula is given by:
Vcone = pir2H
3
Know more: Cube and parallelepiped volume: learn how to calculate
solved exercises
Question 1 – A straight cone has a generatrix equal to 5 cm and a height of 3 cm. Determine the averages of the total area and volume of this cone.
Solution
Initially, we draw this cone with the data provided.
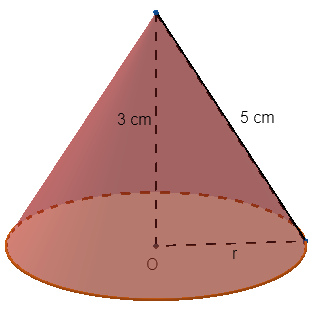
To find the value of the area and volume of the cone, it is first necessary to determine the radius value of the base. For this, we will use the Pythagorean Theorem.
52 = 32 + r2
25 = 9 + r2
25 - 9 = r2
r2 = 16
r = 4 cm
Thus, the area and volume are, respectively:
THEcone = πr (g + r) ⇒ Acone = 4π (5 + 4) ⇒ Acone = 36π cm2
Vcone = pir2H ⇒ Vcone = π423 ⇒ Vcone = 16π cm3
3 3