Every function of form f (x) = ax² + bx + c, on what The, B and ç are real numbers and The different from 0, it is called quadratic function or 2nd degree polynomial function.
Let's determine the function that represents the following situation: João has a land whose sides measure 10 m and 25 m, this land is on a corner. The city hall will increase the width of the sidewalks in x meters, therefore it will reduce the area of João's land.

Note that the terrain is represented by a rectangle, so let's relate the side measurements to the formula for calculating the area of a rectangle:
A(x) = (10 -x). (25-x)
A(x) = 250 -10x -25x + x²
A(x) = x² - 35x + 250
In this function we have: x is the independent variable, the coefficients are a= 1, b= -35 and c = 250.
The graph of a quadratic function is a curve called a parabola.
Let's graph the function: f (x)= x² + 5x +6
First we assign values to x and then we substitute in the function:
x |
Y=f(x) |
-4 |
F(-4) = -4² +5(-4) + 6= 2 |
-2 |
F(-2) = -2² + 5(-2) +6 = 0 |
-1 |
F(-1) = -1² +5(-1)+ 6 = 2 |
0 |
F(0) = 0² + 5.0 + 6 = 6 |
1 |
F(1) = 1² + 5.1 +6 = 12 |
2 |
F(2) = 2² + 5(2) +6 = 20 |
Now that we have some points where the parabola will pass, let's calculate the vertex of this parabola.
Vx = - B = - 5 = - 2,5
2nd to 2nd
Vy = f (Vx) = -2.5² + 5(-2.5) + 6
Vy = 6.25 - 12.5 + 6
Vy = – 0,25
Since a > 0, the concavity of the parabola is facing up:
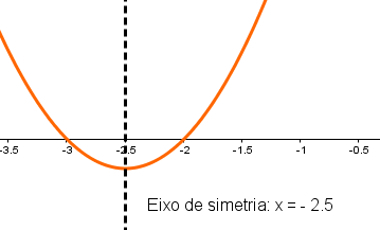
Note that the axis of symmetry was determined by the point x= -2.5; the vertex of the parabola (-2.5; -0.25) and the other points are the coordinates where the parabola passes.
by Camila Garcia
Graduated in Mathematics

