You numbersdecimals are characterized by having an integer part and a decimal part separated by a comma. Generally speaking, we say that decimal numbers are not integers, as they represent "broken" quantities, that is, fractional parts of something whole. In addition, every finite decimal number is periodic tithe have fractional representations.
Read too: What is the value of a digit?
What are decimal numbers?
Decimal numbers have as main characteristic the presence of the comma. As well as the nakedwhole meres, the decimals also use the decimal numbering system, that is, we can differentiate the numbers by the position in which the digits lie.
Decimal numbers often appear in our daily lives, such as when shopping in a supermarket or filling up a car. Thus, it is important to understand how the position system works and, consequently, the nomenclature of these numbers. See the examples:
Let's look at the number 5.4561.
5 → Whole part
4 → tenths
5 → Hundredths
6 → Thousandths
1 → Tenth of Thousandths
Note that the digit 5 appears twice in the number, however, it represents different quantities. The 5 (integer part) indicates 5 units, while the numbers to the right of the comma represent fractions of an integer. Thus, the reading of the number must be done as follows:
Five integers, four thousand, five hundred and sixty-one tenth of thousandths
Example 1 – Analyze each digit of the number 7.143 and write it out in full.
7,143 = 7 + 0,1 + 0,04 + 0,003
7 → Whole part
0.1 → tenths
0.04 → Hundredths
0.003 → Thousandths
Therefore, the reading of the number is:
Seven integers and one hundred and forty three thousandths
Note that, to the left of the comma, the entire part is always found. Note now that when the digit zero is added to tenths, hundredths, thousandths, and so on, the number does not change as long as there is no number to the right of that zero. Look:
3,000 = 3
5,0 = 5
See too: Decimal numbering system - system that uses the number 10 as the base
Operations with decimal numbers
Addition
The addition of decimal numbers is defined as the addition of whole numbers. We must add whole part to whole part, tenths to tenths, hundredths to hundredths and so on. In other words, we must put comma below comma. See the example:

Subtraction
THE subtraction between two decimal numbers is the same as adding whole numbers. We operate whole part to whole part, tenths to tenths, and so on. See the example:

Multiplication
THE mmultiplication between two decimal numbers is performed similarly to the multiplication of whole numbers. At end we add the number of decimal places of the two numbers and we put those decimal places in the result.

Division
To carry out the division between decimal numbers, we need to equal the decimal places by multiplying the two numbers by powers of ten, that is, ten, a hundred, a thousand, and so on. After the decimal places are equal, division is performed in the same way as for whole numbers.
Decimal numbers in fraction

To write a decimal number in its fractional form, we must keep number without comma in numerator gives fraction and put the base 10 power in the denominator, that is, we must place the numbers ten, one hundred, one thousand and so on according to the number of decimal places that we “walk” to make the decimal number a whole number. See the example:
Let's turn the number 0.43 into its fractional form. Note that the number without the comma is written as follows: 043, that is, 43. Also note that, to ignore the comma, it was necessary to "walk" two decimal places, so we must divide the 43 by 100.

Also access: Minimum common multiple - device used to match denominators
solved exercises
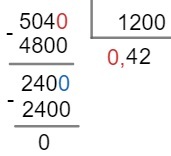
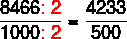
question 1 – Write the decimal number 8.466 in its fractional form.
Resolution:
The first step is to “eliminate” the comma. For this, it is necessary to "walk" three decimal places.
8,466
We should divide the number 8466 by 1000:
question 2 – A package of soap with 4 bars costs R$ 2.88. How much does each bar of soap cost?
Resolution
We know that the 4 bars cost BRL 2.88, so to determine the price of each one, we must divide the total price of the package by 4.
2,88 ÷ 4
To perform the operation, it is necessary to equal the decimal places. For that, let's multiply by 100 both sides of the split.
2,88 (x 100) ÷ 4 (x 100)
288 ÷ 400
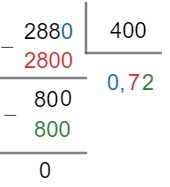
Therefore, each soap costs R$0.72.