THE potentiation is a mathematical operation that represents the multiplication successive number by itself. By multiplying the 3 by itself 4 times, this can be represented by the power 3 raised to 4: 34.
This operation has important properties that facilitate the calculation of powers. Just as multiplication has division as an inverse operation, the potentiation has rooting as an inverse operation.
Each element of the enhancement is given a specific name:
Theno = B
the → base
n→ exponent
b→ power
Read too: Potentiation and fractionation of fractions
How to read a power?

Knowing how to read a powerhouse is an important task. The reading is always done starting with the number in the base raised to the number in the exponent, as in the following examples:
Examples:
a) 4³ → Four to the three, or four to the third power, or four to the cube.
b) 34 → Three to the four, or three to the fourth power.
c) (-2)¹ → Minus two to the one, or minus two to the first power.
d) 8² → Eight to the two, or eight to the second power, or eight to the square.
Powers of exponent 2 can also be called powers squared, and powers of degree 3 can be called powers cubed, as in the previous examples.
Power calculation
To find the value of a power, we need to perform multiplications as in the following examples:
a) 3²= 3 · 3 = 9
b) 5³= 5·5·5 = 125
c) 106 = 10 · 10 · 10 · 10 · 10 · 10 = 1 000 000
Power Types
There are some specific types of power.
1st case – When the base is non-zero, we can say that every number raised to zero is equal to 1.
Examples:
a) 100=1
b) 12930=1
c) (-32)0=1
d) 80=1
2nd case - Every number raised to 1 is itself.
Examples:
a) 9¹ = 9
b) 12¹ = 12
c) (-213)¹= - 213
d) 0¹ = 0
3rd case - 1 to any power is equal to 1.
Examples:
a) 1²¹ = 1
b) 1³ = 1
c) 1500=1
4th case - Basis of a negative potentiation
When the base is negative, we separate it into two cases: when the exponent is odd, the power will be negative; when the exponent is even, the answer will be yes.
Examples:
a) (-2)³ = (-2) · (-2) · (-2) = - 8 → Note that the exponent 3 is odd, so the power is negative.
b) (-2)4= (-2) · (-2) · (-2) · (-2) = 16 → Note that the exponent 4 is even, so the power is positive.
Read too: Powers with negative exponent
Power with negative exponent
To calculate the power with negative exponent, we write the inverse of the base and change the sign of the exponent.
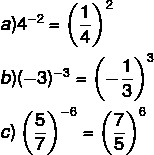
Enhancement Properties
In addition to the types of enhancement shown, enhancement has properties important to facilitate the power calculation.
→ 1st property - Multiplication of powers of the same base
When we perform a multiplication of powers of the same base, we keep the base and add the exponents.
Examples:
The) 24·23 = 24+3=27
b) 5³ ·55 · 52= 53+5+2 = 510
→ 2nd property – Power division of same base
When we find a power division of the same base, we keep the base and subtract the exponents.
Examples:
a) 37: 35 = 37-5 = 32
b) 23 : 26 = 23-6 = 2-3
→ 3rd property - Power power
When calculating the power of a power, we can keep the base and multiply the exponents.
Examples:
a) (5²)³ = 52·3 = 56
b) (35)4 = 35·4 = 3 20
→ 4th property - Power of a product
When there is a multiplication of two numbers raised to an exponent, we can raise each of those numbers to the exponent.
Examples:
a)(5 · 7)3 = 53 · 73
b)(6·12)8 = 68 · 128
→ 5th property - Ratio power
To calculate powers of a quotient or even a fraction, the way to perform is very similar to the fourth property. If there is a division raised to an exponent, we can calculate the power of the dividend and the divisor separately.
a) (8:5)³ = 8³: 5³

Potentiation and Radiation
THEradiciation is the reverse operation of potentiation, that is, it undoes what was done by power. For example, when we calculate the square root of 9, we are looking for the number squared that makes 3. So, to understand one of them, it is essential to master the other. In equations, it is also quite common to use radiciation to eliminate a potency of an unknown, and also the opposite, that is, to use potentiation to eliminate the square root of an unknown.
Example
- Calculate the value of x, knowing that x³ = 8.
In order to calculate the value of x, it is necessary to carry out the inverse operation of the potentiation, that is, the radiciation. In reality, we are looking for the number that, when cubed, results in the number 8.

This relationship between rooting and potentiation makes it essential to master potentiation rules to advance learning about rooting.
Read too: How to calculate roots using powers?
solved exercises
1) (PUC-RIO) The highest number below is:
a) 331
b) 810
c) 168
d) 816
e) 2434
Resolution:
Performing the comparison by calculating each one of them would be a difficult task, so let's simplify the alternatives,
a) 331 → is already simplified
b) 8 = 2³ → (2³)10 = 230
c) 16 = 24 → (24)8 = 232
d) 81 = 34 → (34)6 = 324
e) 243=35 → (35)4 = 320
Therefore, the greatest power is the letter A.
2) The simplification of the expression [310: (35. 3)2]- it's the same as:
a) 3-4
b) 34
c) 30
d) 3²
e) 3-2
Resolution:
[310: (35. 3)2]-2
[310: (36)2]-2
[310: 312]-2
[3-2]-2
34
Letter B.