By learning about the division operation, we know that there are exact divisions and non-exact divisions (when there is a remainder in the division). For example, if we want to divide 5 by 2, we have an inexact division, as there will be a remainder.
But is there a possibility to end this division? If you have five reais, is it possible to split this amount for two friends? Of course! Each friend will earn two reais and fifty cents. The “one real” that would remain in the rest was divided equally and now there are no more remains in that division.
Let's look at another calculation similar to this one: the division of 225 per 50. if we multiply 4 per 50, we will get 200, and so the division will have remainder 25. There is no natural number that multiplied by 50 result in 25, so whatever value we add to the quotient will be less than 1. So, in order to proceed, we will have a comma division, because we will add a comma to the quotient and a zero to the rest. We are now looking for a number that multiplied by 50 results in 250. This number is the 5. Therefore, 225: 50 = 4,5.
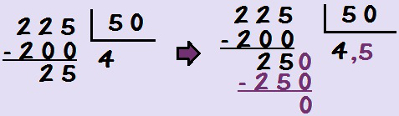
So that there is no remainder in the division, we add the comma to the quotient to continue a division that would be inexact
Let's now perform the division of 201 per 4. This is also a non-exact division and will leave rest 1. When we are close to finishing the division and we find the remainder, it will be necessary to add a comma to the quotient and a zero to the end of the remainder. From there, just carry out the division normally until there is no remainder. In this case, there is a comma division, since the division of 201 per 4 results in 50,25.

Again, so that there is no remainder in the division, we add a comma to the quotient to complete the division.
But what about when the dividend or divisor is a decimal number (with a comma)? We need to remember that a decimal number only divides or is divided by another decimal number if there are the same number of digits after the decimal point..
If one of the division factors is a decimal number, we must write the other one in decimal form as well. For example, the number 2 can be written as 2,0; 2,00; 2,000...
Let's see how to perform the division of 3,4 per 2. The first step is to note that, as the 3,4 is a decimal number with a digit after the comma, O 2 must have this same format, that's why we use the 2,0 on the divider. Now that both division factors have the same number of digits after the decimal point, we can disregard the commas and perform the division of 34 per 20, getting as a result 1,7. See the entire process to carry out this division in the image below:

We need to write the divisor in decimal form with a digit after the comma and then discard the commas and perform the division
Imagine a new situation: in the dividend, there is the natural number 30, and on the divisor, a rational number 2,5. Remember that a decimal number only divides or is divided by another decimal number if they both have the same number of digits after the decimal point.
To perform the division, let's write the number 30 in the form 30,0. Now that the dividend and the divisor have a number after the comma, we can disregard the commas and perform the division between 300 and 25, obtaining as a result the quotient 12, as we can see in the following figure. Note that a comma division can result in a non-comma quotient!

Now we must write the dividend in decimal form with a digit after the comma and then perform the division
And when the dividend and the divisor are decimal? In this case, we just need to match the number of digits after the decimal point in both factors, completing with zeros as necessary. For example, when dividing 31,775 per 15,5, we need to add two zeros to the divisor so that both have three digits after the comma. Once this is done, we disregard the commas and perform the division of 31775 per 15500, obtaining the quotient of the number 2,05, as we can see in the following example:

In this case, we must write the dividend and the divisor with the same number of digits after the comma and then disregard the commas
By Amanda Gonçalves
Graduated in Mathematics

