THE periodic tithe is a number that has its decimal infinite and periodic part, that is, in its decimal part, there is a number that repeats itself infinitely. considered a rational number, it can be represented as a fraction, which is called generating fraction. It can also be simple or composite.
Read too: fraction division
Representation of the periodic tithe
In addition to the fraction form, known as the generating fraction, the periodic decimal can be represented as a two-way decimal number. We can insert, at the end of the number, ellipsis (…) or we can put a dash above your period (part that is repeated in the tithe), so the same tithe can be represented in two ways. Examples:


simple periodic tithe
A simple periodic decimal has a whole part (which comes before the comma) and the time course, which comes after the comma.
Examples:
1,333…
1→ entire part
3 → period
0,76767676…
0 → whole part
76 → period
compound periodic tithe
A composite periodic decimal has whole part (which comes before the comma), non-periodic part and time course, which comes after the comma. What differentiates a simple periodic decimal from a composite one is that, in the simple one, there is only the period after the comma; in compound, there is a part that does not repeat after the comma.
Examples:
1,5888…
1 → whole part
5 → non-periodic part
8→ period
32,01656565…
32 → entire part
01 → non-periodic part
65 → period
Read too:Decimal numbers – learn to perform math operations with these numbers
generating fraction
Finding the fraction that generates the tithe is not always an easy task. We need to divide it into two cases: when the tithe is simple and when it is compounded. To find the generating fraction, we use an equation.
→ Generative fraction of a simple periodic decimal
Example:
- Let's find the generating fraction of the 1.353535 tithe…
Let x = 1.353535…, as this tithe has 2 numbers in its period (35), let's multiply x by 100. Then,
100x = 135.3535...
Now performing the subtraction,

There's one practical method to find the generating fraction of a simple periodic decimal that avoids the construction of equations. Let's find again the generating fraction of the 1.353535 tithe…, but by the practical method.
1st step: identify period and whole part.
Whole part → 1
Period → 35
2nd step: find the numerator.
The numerator is the number formed by the integer part and the period (in the example, it is 135) minus the integer part, that is:
135 – 1 = 134
3rd step: find the denominator.
For that, let's evaluate how many numbers there are in the tithe period, and for each number, we'll add the number 9 in the denominator. Since in this case there are two numbers, the denominator is 99. Therefore, the generating fraction is:

→ Generative fraction of a composite periodic decimal
A little more complicated to find, the generating fraction of a composite periodic decimal can also be determined by means of a equation.
Example:
- Let's find the generating fraction of the 2.13444 decimal...
Let x = 2.13444…. let's multiply by 100 so that, after the comma, only the periodic part remains. Then,
100x = 213,444….
On the other hand, we know that 1000x= 2134.444….
Now we will do the subtraction:

For the compound periodic decimal, there is also a practical method, which we're going to use to find the generating fraction of the composite periodic decimal 2,13444…
1st step: identify the parts of the periodic tithe.
Whole part→ 2
Non-periodic part → 13
Period →4
2nd step: find the numerator.
To calculate the numerator, let's write the number formed by the integer part, non-periodic part and period, that is, 2134 minus the whole part and the non-periodic part, that is, 213.
2134 – 213 = 1921
3rd step: find the denominator.
In the denominator, for each number in the period, we add a 9and for each number in the non-periodic part, a 0.In the example, the denominator is 900.
The generating fraction is:
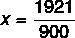
Read too: Comma division – how to do it?
solved exercises
1) Of the following numbers, mark the one that corresponds to a composite periodic decimal.
a) 3.14159284...
b) 2.21111
c) 0.3333….
d) 1,21111….
Resolution:
Alternative D.
Analyzing the alternatives, we have to:
a) It is a non-periodic tithe. Realize that, as infinite as it is, there is no way to predict the next numbers.
b) It is not a tithe.
c) It is a simple periodic decimal.
d) True, as it is a compound periodic decimal.
2) The generating fraction of the 12,3727272 tithe… is it ?
a) 1372/9999
b) 12249/990
c) 12/999
d) 123/990
Resolution:
By the practical method, we have: 12372 – 123= 12249, which will be the numerator.
Analyzing the decimal part:
3 → non-periodic part
72 → period
990→ denominator
The fraction that best represents is 12249/990, letter B.

