One triangle is figuregeometric which has three sides, three angles and three vertices. You triangles have several properties, one of them concerns their inner angles: regardless of the triangle's dimensions, its shape, the length of its sides or the measurement of its internal angles, the sum of these internal angles will always be equal to 180°.
In other words, if ABC is a triangle, and a, b, and c are your anglesinternal, as we can illustrate with the following image:
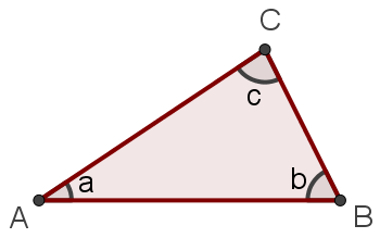
So, we can correctly write the sum:
a + b + c = 180°
Generally, this equality is not used to find that the sumFromanglesinternal of a triangle is equal to 180°, but to determine the measure of one of the internal angles of a triangle. triangle, when the measurements of the other two are known.
Example: What is the measurement of the third internal angle of a triangle which has two internal angles equal to 30° and 90°?
Solution:
30° + 90° + x = 180°
x = 180° - 30° - 90°
x = 60°
The third angle measures 60°.
Demonstration
Consider the triangle ABC, with angles a, b and c, like the one in the following figure:

Build on point C a parallel straight beside AB of this triangle.
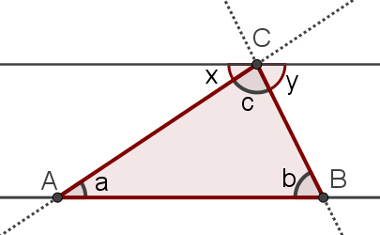
Line parallel to side AB in triangle ABC
Note that sides AC and BC can be thought of as cross straights, which cut the two parallel lines. You angles x and y formed in this construction are, respectively, internal alternating with angles a and b. Thus, x = a and y = b.
Now, notice that the sum x + c + y = 180°, because the three angles are adjacent and their limits are the line parallel to side AB. So, substituting the values of x and y, we will have:
a + b + c = 180°
Examples:
1st Example – Determine the measurement of each of the three anglesinternal of triangle Next.
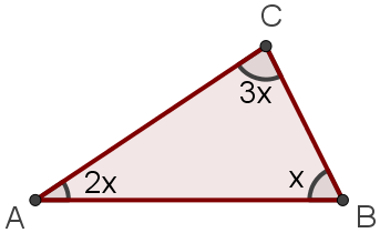
Solution:
Knowing that the sum of anglesinternal on one triangle is equal to 180°, just do:
x + 2x + 3x = 180°
6x = 180°
x = 180°
6
x = 30°
Like the anglesinternal are multiples of x, each of them measures:
x = 30°,
2x = 60° and
3x = 90°
2nd Example - One triangle have one of yours anglesinternal with the measure exactly equal to three times the measures of the other two, which are congruent. How long are each of the internal angles of this triangle?
Solution:
To solve this problem, assume that the two congruent angles measure x and the other angle measures 3x. as the sum of anglesinternal is equal to 180°, we will have:
x + x + 3x = 180°
5x = 180°
x = 180°
5
x = 36°.
How x is the measure of the two angles congruent, we already know that they measure 36°. The third angle is triple that, so it measures:
3x = 3·36 = 108°
Related video lesson:



