You know what it is MDC? The acronym MDC stands for Maximum Common Divider. If we think of two numbers or more, there are one or more values that divide those numbers, and the division leaves no remainder. For example, consider the numbers 30 and 12, let's identify the divisors of each number:
D (30) = {1, 2, 3, 5, 6, 10, 15, 30}
D (12) = {1, 2, 3, 4, 6, 12}
The 12 and the 30 have some common dividers, they are the 2, 3 and 6. O bigger theirs is the 6. For this reason, we say that the maximum common divisor between 30 and 12 is 6 or simply, MDC (30, 12) = 6.
But there are other ways to find the MDC between these numbers. Let's comment now on the successive divisions method. In this method, we divide the largest number by the smallest. For the last example, we we will divide 30 by 12. By making this division, we will find remaining 6. We will then do another division, the number that was in the divider will become dividend, and what was in the rest will become divider. We will have the following exact division that leaves no remains: 12 divided by 6. As this division is exact, we say that the number that was last in the divisor, in this case the 6, and the maximum common divisor between 30 and 12. See below this entire process:

Finding the MDC (12, 30) through the successive divisions method
The divisions should be done as many times as necessary until we finally find the division that leaves zero remainder. Let's look at the process for identifying the maximum common divider between 54 and 16. As the 54 is bigger, we make the division of 54 by 16, which leavesrest 6. We then do the 16 by 6 division, which leaves remainder 4. We repeat the process now with the 6 by 4 division, which leaves remainder 2. Lastly, we divide 4 by 2, getting rest 0. Therefore, the MDC (54, 16) = 2. Follow the process of successive divisions below to find the greatest common divider between 54 and 16:
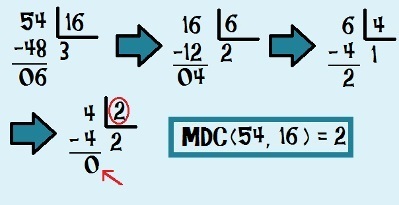
Finding the MDC (54, 16) through the successive divisions method
And when do we want to find the greatest common divisor between three or more numbers? Through the same process, we will choose two numbers to apply the successive divisions method until we find the MDC between those numbers. When we find it, we'll divide the other number and check if it's also a divisor of the third number. It is possible to repeat the process of successive divisions as many times as necessary. Below, we can see the application of the procedure to find the MDC (9, 15, 27):
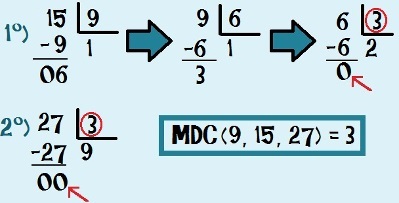
Finding the MDC (9, 15 and 27) through the successive division method
By Amanda Gonçalves
Graduated in Mathematics