At straight they are lines that do not curve and are formed by infinite points for the two directions in which they extend. They must be defined within a plan and, by taking two or more, it is possible to analyze the position from one to the other: the calls relative positions between straight lines.
The analysis of positions of geometric figures also extends to the relative positions between point and line, lines and planes, plane and plane, line and circumference etc.
Parallel Lines
Two straight are called parallel when they have no common point, that is, in all their infinite extension, there is no meeting point between them. A good illustration for parallel lines, although it is impossible to show them in full, it is as follows:

Two parallel lines: do not have a common point
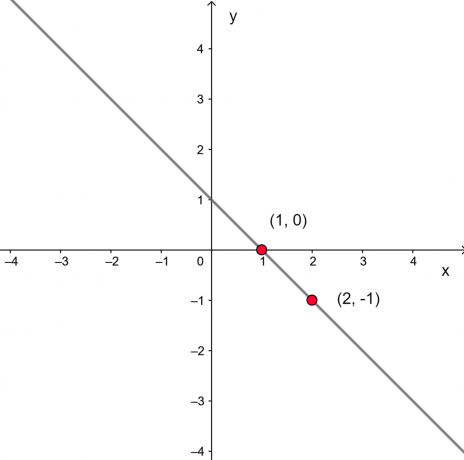
Competing lines
two (or more) straight are called competitors when they have a single point in common. In this case, a angle between them. When this angle is 90°, we say that the lines are perpendicular.

Two competing straight lines: they have only one meeting point
So whenever two straight are perpendicular, they are also competitors. However, not always that two lines are concurrent, they are perpendicular.
The most interesting property of the competing straight lines it concerns its angles: adjacent angles are supplementary (the sum of supplementary angles is equal to 180°) and angles opposed by the vertex (the meeting point of the two lines) are equal.
Coincident lines
two (or more) straight are called coincident when they have two or more points in common.
The ownership of these straight is as follows: If two lines have at least two points in common, then they have all points in common. Look at the image below. Note that it is not possible for two distinct lines to have two points in common.

Coincident lines: Lines that have two and therefore all points in common
By Luiz Paulo Moreira
Graduated in Mathematics
Related video lesson: