One first degree function, or affine function, is any function that can be described as follows:
f (x) = ax + b
Where The and B are any real numbers.
the variable x is called an independent variable, and the set of numbers that variable takes is called the domain of the function. About that, y = f(x) is called the dependent variable, and the set of numbers that y assumes is called the counterdomain.
Examples of First Degree Functions:
a) 2x + 1 → a = 2 and b = 1
b) -x + √9 → a = -1 and b = √9
c) 5x → a = 5 and b = 0
Note that in all these functions the exponent of the independent variable is 1, that is, x¹ = x. Functions with an exponent other than 1, such as x² – 3, are not first-degree functions.
Graph of a function of the first degree
O graph of a function of the first degree is always a line, what will change from one function to another is the slope and location of the line on the Cartesian plane, which will depend on the values of The it's from B.
Remember that a single line passes through two points, so to graph a function of the first degree, just find two ordered pairs that belong to this line.
To find these two ordered pairs, just choose two values for x and substitute into the function to find the y values.
Example: Build the graph of the function f (x) = – x + 1.
For x = 1, we have f (1) = -1 + 1 = 0, so we have the ordered pair (1, 0).
For x = 2, we have f (2) = -2 + 1 = -1, so we have the ordered pair (2, -1).
Now, we build the Cartesian plane and mark these two points, drawing a straight line that passes through them:

Ascending function and descending function
The function of the first degree can be a increasing function or a descending function, it will depend on the value of The.
- if The is a positive value (a > 0), the function is increasing.
- if The is a negative value (a < 0), the function is decreasing.
- Free Online Inclusive Education Course
- Free Online Toy Library and Learning Course
- Free Online Preschool Math Games Course
- Free Online Pedagogical Cultural Workshops Course
In an increasing function, as the value of x increases, the value of y also increases. In a decreasing function, when x increases, y decreases, or vice versa.
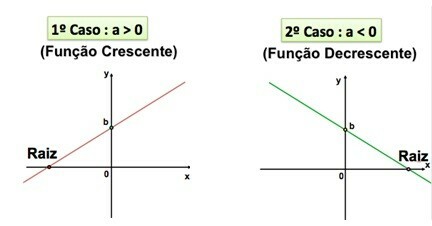
As the slope of the line depends on the value of The, this value is also called slope. Already the value of B, is the value where the line crosses the y axis, so it is called linear coefficient.
So, in a function f(x) = ax + b, we have:
- a: is the slope.
- b: is the linear coefficient.
Another observation is that the value where the line crosses the x-axis is called the root or zero of the first degree function.
First degree function root
The root or zero of a function of the first degree is the value that x takes when y equals zero. So, to determine the root of a function, just equate the function to the value 0 and find the value of x.
Examples: Find the root of the functions below.
a) f (x) = 2x – 6
2x - 6 = 0
2x = 6
x = 6/2
x = 3
So the root of this function is 3.
b) f (x) = -x + 0.5
-x + 0.5 = 0
-x = -0.5
x = 0.5
So the root of this function is 0.5.
You may also be interested:
- First degree equation
- systems of equations
- Inequalities - First and Second Degree
The password has been sent to your email.


