O least common multiple, denoted by MMC, of two or more positive integers is the smallest non-zero number that appears in the list of multiples of these two or more numbers at the same time.
There is a method that facilitates the calculation of the least common multiple of a number and, to use it, it is necessary to remember the prime factor decomposition, formally known as the Fundamental Theorem of Arithmetic. Such theorem assures us that every composite number can be written as a product of prime factors.
Read too: Do you know the properties of multiplication?

common multiple
When we have two or more positive integers, it is possible to list multiples of those numbers. When we carry out this listing, we will notice that there are more than one multiple in common, that is, multiples appearing at the same time in all lists of these given numbers. See the example.
Example - Listing of the 10 first multiples of numbers 2, 8, 10.
M(2) = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, ...}
M (8) = {8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...}
M (10) = {10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...}
We can see more than one common multiple between the numbers. Note that, between M (2) and M (8), we have in common the numbers 8, 16, 24...; between M (2) and M (10), we have the numbers 10, 20, 30,...; between M (8) and M (10), we have the numbers 40, 80,... These numbers are called common multiples.
How to determine the MMC?
To determine the MMC, we must initially list some multiples of the numbers in question. The first multiple that appears in listing the two or more numbers in question is called the least common multiple. It is called the minimum because it is the smallest of them and will always match the first number common to the two or more numbers.
Example - To determine the least common multiple between the numbers 4 and 8, let's list the multiples of the two numbers.
M (4) = {4, 8,12,16, 20, ...} and M (8) = {8, 16, 24,32,40, ...}
Now, notice that the smallest multiple that appears in both listings is the number 8. Therefore, the MMC (8.4) = 8
realize that this method is not practicalwhen the numbers are too big. Imagine, for example, determining the MMC between the numbers 2 and 121 using this method. We would have to list the multiples of 2 until we get close to 121.
With this in mind, we can use the prime factor decomposition, that is, we must carry out successive divisions by Prime numbers. See the following example.
To calculate the MMC (121,2), we will initially decompose the number into prime factors and then multiply those factors. The result of the multiplication will be the MMC.

Thus, the MMC (121,2) = 2 ·11 ·11 = 242.
Example - Determine the MMC (8.4) using prime factor decomposition.

Hence, the MMC (8.4) = 2 · 2 ·2 = 8, as shown by the first method.
MMC Properties
See the properties of the MMC below.
Property 1
The product of the greatest common divisor with the least common multiple of two numbers The and B is equal to the modulus of the product of these numbers.
MDC (a, b) · MMC (a, b) = |a · b|
Example - We know that the MDC (8.4) = 4 and MMC (8.4) = 8. In fact,
MDC (8.4) · MMC (8.4) = | 8 · 4 |.
Property 2
Common multiples of two or more numbers are MMC multiples of those numbers.
Example - We saw that M (4) = {4, 8,12,16, 20, ...} and M (8) = {8, 16, 24,32,40, ...} and that the MMC (8.4) = 8. The property tells us that the multiples of 8 and 4 are multiples of 8, which, coincidentally in this case, is the least common multiple.
Property 3
The MMC between two prime numbers of each other is equal to the multiplication between them.
NOTE: Two numbers are prime to each other when they have no common divisor.
Example - Find the least common multiple between 5 and 21.
As the numbers do not have a common divisor, that is, they are cousins to each other, the smallest multiple between them is the product between them, thus MMC (21.5) = 21 · 5 = 105. In fact, this is true, as we can see from the decomposition into prime factors.

MMC (21.5) = 3 ·5 ·7 = 105
Read too: Highest common divisor: what is it and what is it for?
MMC and fractions
O least common multiple is also used to perform the operations of addition and subtraction of fractions. For add or subtract two or more fractions, simply first calculate the MMC between the denominators, then divide that MMC by the denominator and multiply the result by the numerator. See the examples.
Example – Determine the sum of the following fraction 4 + 5.
7 3
Initially let's determine the MMC (7,3). For this, we can use the property 3, thus, MMC (7.3) = 21.

Thus, 4 + 5 = 56 :7 = 8.
7 3 21:7 3
The same procedure is valid for when we have a subtraction of fractions, just pay attention only to the sign between the fractions.
Read too: Operations with fractions: learn how to do it
Exercise solved
Question 1 – (UPE) Rodrigo was watching the blinker on his home's Christmas ornament. It consists of bulbs in yellow, blue, green and red. Rodrigo noticed that the yellow light bulbs light every 45 seconds, the green light bulbs every 60 seconds, the blue, every 27 seconds, and the red ones only light up when the lamps of the other colors are lit at the same time. How many minutes do the red lamps light up?
The) 6
B) 9
ç) 12
d) 15
and) 18
Solution
As the lamps only light up when all are on the Same time, that is, we must find the common time of activation of the lamps. So, just calculate the MMC between 60, 45 and 27.
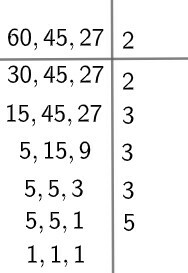
Hence, the MMC (60, 45, 27) = 2 x 2 x 3 x 3 x 3 x 5 = 540 seconds. As the exercise is interested in the time interval in minutes, just divide the 540 by 60.
540: 60 = 9 minutes.
Alternative b.



